(→Introduction) |
|||
| Line 11: | Line 11: | ||
* [[LBG_Old Kiwi]] | * [[LBG_Old Kiwi]] | ||
* Fuzzy C-means | * Fuzzy C-means | ||
| − | * Hierarchical | + | * [[Hierarchical clustering_Old Kiwi]] |
| − | * Mixture of | + | * [[Mixture of Gaussians_Old Kiwi]] |
* [[Genetic algorithm_Old Kiwi]] based clustering | * [[Genetic algorithm_Old Kiwi]] based clustering | ||
An important component of a clustering algorithm is the distance measure between data points. If the components of the data instance vectors are all in the same physical units then it is possible that the simple Euclidean distance metric is sufficient to successfully group similar data instances. However, even in this case the Euclidean distance can sometimes be misleading. Figure shown below illustrates this with an example of the width and height measurements of an object. Despite both measurements being taken in the same physical units, an informed decision has to be made as to the relative scaling. As the figure shows, different scalings can lead to different clusterings. | An important component of a clustering algorithm is the distance measure between data points. If the components of the data instance vectors are all in the same physical units then it is possible that the simple Euclidean distance metric is sufficient to successfully group similar data instances. However, even in this case the Euclidean distance can sometimes be misleading. Figure shown below illustrates this with an example of the width and height measurements of an object. Despite both measurements being taken in the same physical units, an informed decision has to be made as to the relative scaling. As the figure shows, different scalings can lead to different clusterings. | ||
| − | |||
== References and Bibliography == | == References and Bibliography == | ||
Revision as of 14:34, 6 April 2008
Introduction
Clustering is a nonlinear activity that groups data by generating ideas, images and chunks around a stimulus point. As clustering proceeds, the groups enlarge in size, and one is able to visualize patterns and ideas. Clustering may be a class or an individual activity.
The diagram below gives a simplistic representation of clustering. Figure I has data, not necessarily grouped, and application of a clustering algorithm results in the formation of clusters or groups, that is shown in the second figure.
Some of the widely used algorithms for clustering include:
- K-means_Old Kiwi
- LBG_Old Kiwi
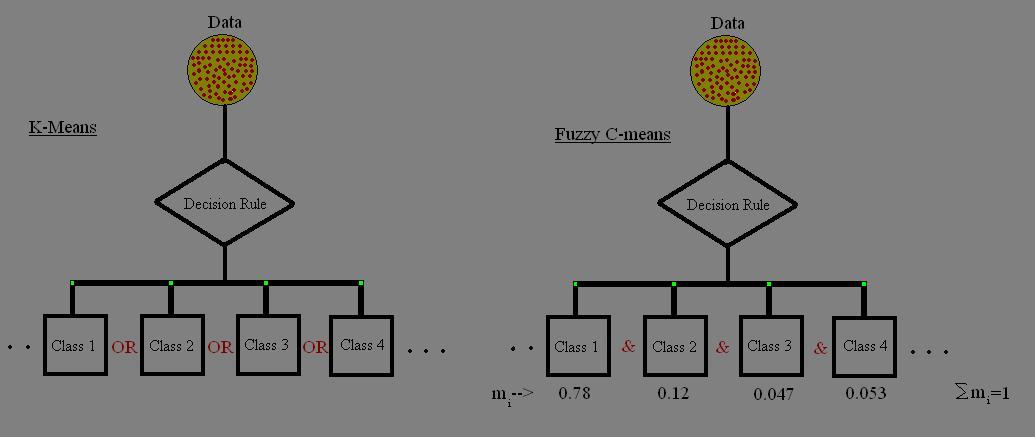
- Fuzzy C-means
- Hierarchical clustering_Old Kiwi
- Mixture of Gaussians_Old Kiwi
- Genetic algorithm_Old Kiwi based clustering
An important component of a clustering algorithm is the distance measure between data points. If the components of the data instance vectors are all in the same physical units then it is possible that the simple Euclidean distance metric is sufficient to successfully group similar data instances. However, even in this case the Euclidean distance can sometimes be misleading. Figure shown below illustrates this with an example of the width and height measurements of an object. Despite both measurements being taken in the same physical units, an informed decision has to be made as to the relative scaling. As the figure shows, different scalings can lead to different clusterings.
References and Bibliography
From Wikipedia:
Survey Papers:
- Survey of Clustering Data Mining Techniques, by Pavel Berkhin [1]
- Survey of Clustering Algorithms, by Rui Xu and Donald Wunsch, IEEE Journal of Neural Networks, Vol 16, May 2005 [2]
