(→Synchronous Demodulation (with phase error) in the Frequency DomainAgain) |
(→Synchronous Demodulation (with phase error) in the Frequency DomainAgain) |
||
| Line 36: | Line 36: | ||
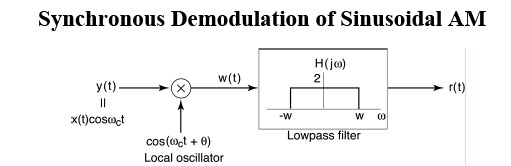
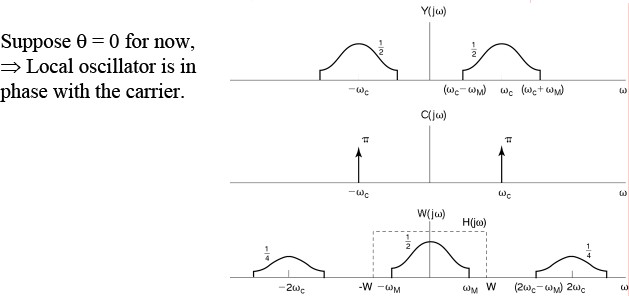
Demodulating signal has phase difference θw.r.t.the modulating signal | Demodulating signal has phase difference θw.r.t.the modulating signal | ||
| − | <math> | + | <math>cos(\omega_{C}t+\theta)= \frac{1}{2}e^{j\theta}e^{j\omega_{c}t}+\frac{1}{2}e^{-j\theta}e^{-j\omega_{c}t}</math> |
| − | ====> <math>/ | + | fourier ====> <math>\pie^{j/theta}/delta(/omega-/omega_{c})+/pie^{-j/theta}/delta(/omerga-/omerga_{c})</math> |
Revision as of 18:59, 17 November 2008
Contents
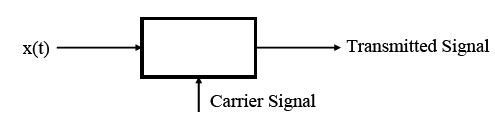
the concept of modulation
•More efficient to transmit E&M signals at higher frequencies
•Transmitting multiple signals through the same medium using different carriers
•Transmitting through “channels” with limited passbands
•Others...
How?
•Manymethods
•Focus here for the most part on Amplitude Modulation (AM)
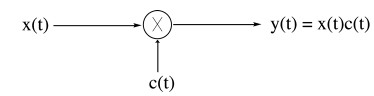
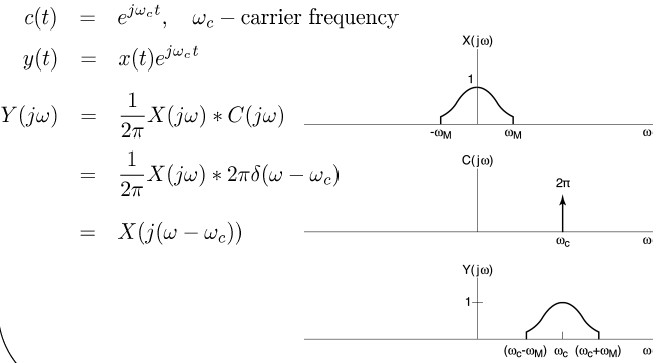
Amplitude Modulatioin of a Complex Exponential Carrier
Demodulation of Complex Exponential AM
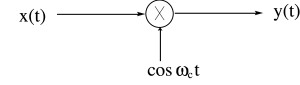
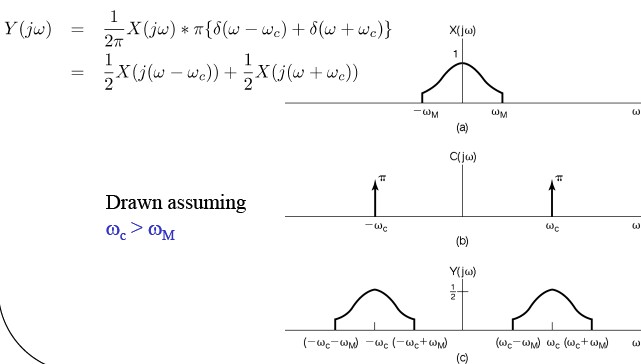
Sinusoidal AM
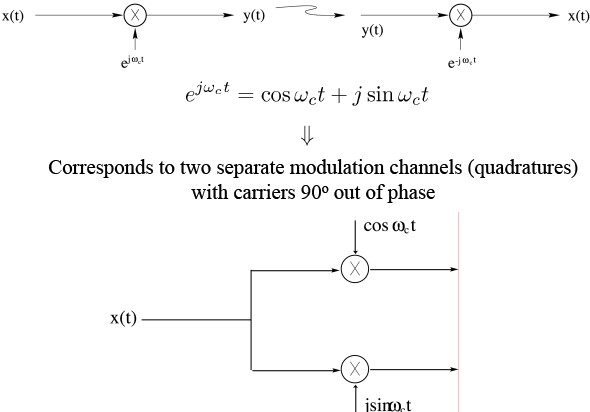
Synchronous Demodulation (with phase error) in the Frequency DomainAgain
Demodulating signal has phase difference θw.r.t.the modulating signal
$ cos(\omega_{C}t+\theta)= \frac{1}{2}e^{j\theta}e^{j\omega_{c}t}+\frac{1}{2}e^{-j\theta}e^{-j\omega_{c}t} $
fourier ====> $ \pie^{j/theta}/delta(/omega-/omega_{c})+/pie^{-j/theta}/delta(/omerga-/omerga_{c}) $