| Line 7: | Line 7: | ||
[[Image:sincos2x_ECE301Fall2008mboutin.jpg]] | [[Image:sincos2x_ECE301Fall2008mboutin.jpg]] | ||
| − | * [[ Matlab Code _ECE301Fall2008mboutin]] | + | * [[Matlab Code _ECE301Fall2008mboutin]] |
Note how much more exciting <math>sin(t)-cos(2t)</math> is than <math>sin(t)</math>. Here the sampling frequency is very small, on the order of <math>10^4</math> | Note how much more exciting <math>sin(t)-cos(2t)</math> is than <math>sin(t)</math>. Here the sampling frequency is very small, on the order of <math>10^4</math> | ||
| + | |||
| + | [[Image:HW2A2_ECE301Fall2008mboutin.jpg]] | ||
| + | |||
| + | * [[Matlab Code _ECE301Fall2008mboutin]] | ||
| + | [[Image:HW2A3_ECE301Fall2008mboutin.jpg]] | ||
| + | * [[Matlab Cide _ECE301Fall2008mboutin]] | ||
Revision as of 14:58, 12 September 2008
Part A: Periodic Signals Revisited...Periodic Signals Revisited...Periodic Signals Revisited
As we discussed in class, a function $ x(t) $ is periodic if $ x(t+T)= x(t) $ , where T is a multiple of the fundamental period, or smallest period.
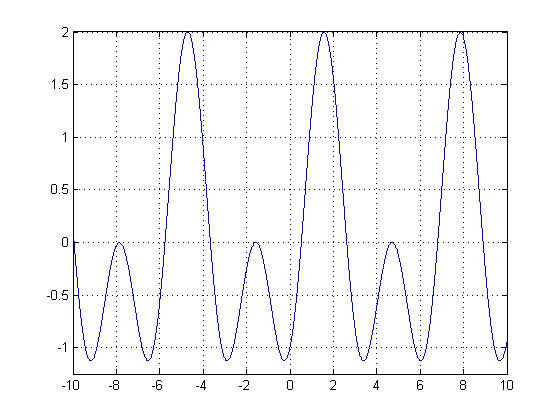
In the first homework, I explained how $ sin(t) $ was periodic. However, because that is rather boring, let's take a look at $ sin(t)-cos(2t) $.
Note how much more exciting $ sin(t)-cos(2t) $ is than $ sin(t) $. Here the sampling frequency is very small, on the order of $ 10^4 $