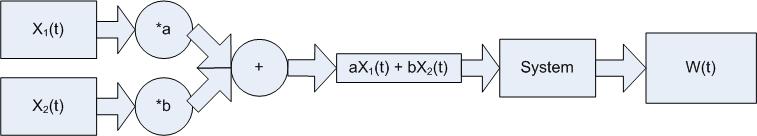(→Definition) |
(→Examples) |
||
| Line 14: | Line 14: | ||
Linear: | Linear: | ||
| + | |||
| + | <math>\ S_{1} = 2x(t + 3) + x(t - 8)</math> | ||
| + | |||
| + | <math>\ S_{2} = x(t - t_{0})</math> | ||
| + | |||
| + | <math>\ S_{1} \rightarrow S_{2} = 2x(t - t_{0} + 3) + x(t - t_{0} - 8)</math> | ||
| + | |||
| + | <math>\ S_{2} \rightarrow S_{1} = 2x(t - t_{0} + 3) + x(t - t_{0} - 8)</math> | ||
| + | |||
| + | |||
| + | Since the results are the same the system is time invariable. | ||
| + | |||
Non-Linear: | Non-Linear: | ||
| + | |||
| + | <math>\ S_{1} = x(-t + 3) - x(-t - 8)</math> | ||
| + | |||
| + | <math>\ S_{2} = x(t - t_{0})</math> | ||
| + | |||
| + | <math>\ S_{1} \rightarrow S_{2} = x(-t + t_{0} + 3) - x(-t + t_{0} - 8)</math> | ||
| + | |||
| + | <math>\ S_{2} \rightarrow S_{1} = x(-t - t_{0} + 3) - x(-t - t_{0} - 8)</math> | ||
| + | |||
| + | |||
| + | Since the results are different they system is time variant. | ||
Revision as of 17:48, 11 September 2008
Definition
If Z(t) and W(t) in the following are equal the system is linear.
Examples
Linear:
$ \ S_{1} = 2x(t + 3) + x(t - 8) $
$ \ S_{2} = x(t - t_{0}) $
$ \ S_{1} \rightarrow S_{2} = 2x(t - t_{0} + 3) + x(t - t_{0} - 8) $
$ \ S_{2} \rightarrow S_{1} = 2x(t - t_{0} + 3) + x(t - t_{0} - 8) $
Since the results are the same the system is time invariable.
Non-Linear:
$ \ S_{1} = x(-t + 3) - x(-t - 8) $
$ \ S_{2} = x(t - t_{0}) $
$ \ S_{1} \rightarrow S_{2} = x(-t + t_{0} + 3) - x(-t + t_{0} - 8) $
$ \ S_{2} \rightarrow S_{1} = x(-t - t_{0} + 3) - x(-t - t_{0} - 8) $
Since the results are different they system is time variant.