(→Example of a Time Invariant System) |
(→Example of a Time Invariant System) |
||
| Line 15: | Line 15: | ||
Let <math>y(t)=2x(t)+2\!</math>. The system is time invarient if for input <math>x(t-t_0)\!</math> the response is <math>y(t-t_0)=2x(t-t_0)+2\!</math>. | Let <math>y(t)=2x(t)+2\!</math>. The system is time invarient if for input <math>x(t-t_0)\!</math> the response is <math>y(t-t_0)=2x(t-t_0)+2\!</math>. | ||
<br> | <br> | ||
| − | |||
| − | |||
<br> | <br> | ||
| + | Proof: | ||
| + | |||
<br> | <br> | ||
[[Image:Timinvar_ECE301Fall2008mboutin.JPG]] | [[Image:Timinvar_ECE301Fall2008mboutin.JPG]] | ||
== Example of a System that is not Time Invariant == | == Example of a System that is not Time Invariant == | ||
Revision as of 12:37, 11 September 2008
Time Invariance
A system is time-invariant if for any input $ x(t)\! $ and any $ t_0\! $ (where $ t_0\! $ is a real number) the response to the shifted input $ x(t-t_0)\! $ is $ y(t-t_0)\! $.
One can show a system is time invarient by proving
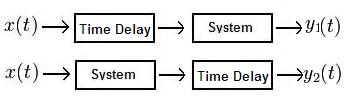
where $ y_1(t)\! $ and $ y_2(t)\! $ are equal.
Example of a Time Invariant System
Let $ y(t)=2x(t)+2\! $. The system is time invarient if for input $ x(t-t_0)\! $ the response is $ y(t-t_0)=2x(t-t_0)+2\! $.
Proof:


