| Line 9: | Line 9: | ||
<center>[[Image:tangent_ECE301Fall2008mboutin.jpg]]</center> | <center>[[Image:tangent_ECE301Fall2008mboutin.jpg]]</center> | ||
| + | |||
| + | |||
By sampling the signal with x[n]=tan[k+n] and k=1.5, it is possible to produce a non-periodic DT signal. | By sampling the signal with x[n]=tan[k+n] and k=1.5, it is possible to produce a non-periodic DT signal. | ||
<center>[[Image:tan_nonperiodic_ECE301Fall2008mboutin.jpg]]</center> | <center>[[Image:tan_nonperiodic_ECE301Fall2008mboutin.jpg]]</center> | ||
| + | |||
| + | |||
| + | By sampling the signal with x[n]=tan[k+n] and k=<math>\frac{\pi/8}</math> | ||
Revision as of 09:30, 11 September 2008
Part A: Periodic Signals Revisited
By sampling a CT periodic signal at different frequencies, one can produce both a periodic and non-periodic DT signal. I chose to use the tangent signal from Homework 1.
$ \tan\theta = \frac{\sin\theta}{\cos\theta}\, $
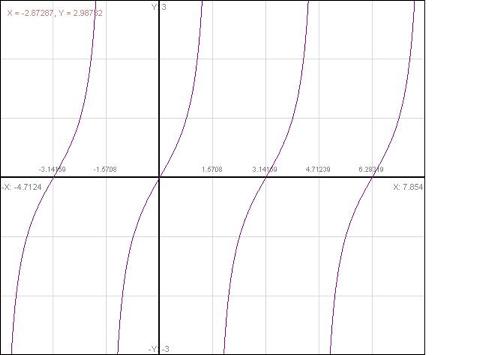
By sampling the signal with x[n]=tan[k+n] and k=1.5, it is possible to produce a non-periodic DT signal.
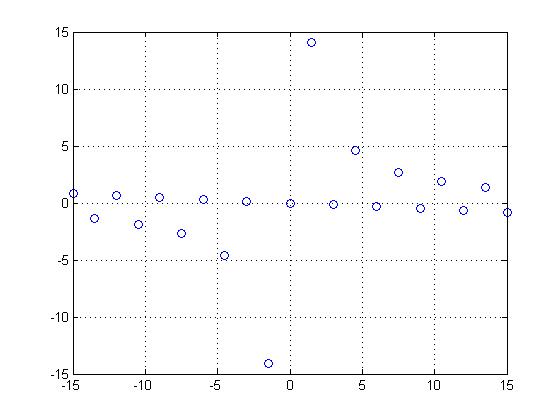
By sampling the signal with x[n]=tan[k+n] and k=$ \frac{\pi/8} $

