(New page: == Periodic Signals == The signal x(t)=sin(t) was chosen: Sampling at a frequency of 1 yields a non periodic signal: Sampling at a frequency of .125*pi yields a periodic signal: Taking...) |
(→Periodic Signals) |
||
| Line 2: | Line 2: | ||
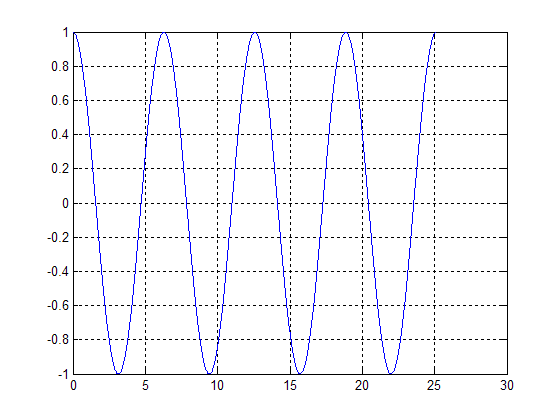
The signal x(t)=sin(t) was chosen: | The signal x(t)=sin(t) was chosen: | ||
| + | |||
| + | [[Image:HW2A1_ECE301Fall2008mboutin.png]] | ||
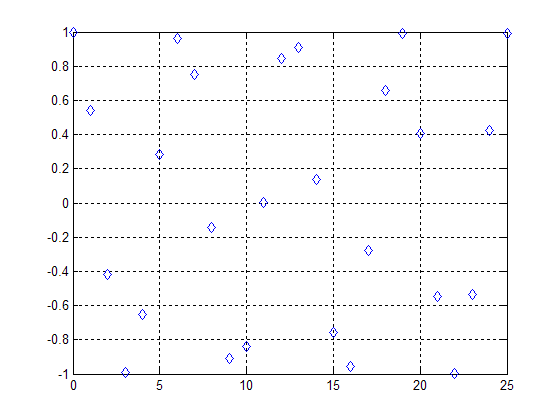
Sampling at a frequency of 1 yields a non periodic signal: | Sampling at a frequency of 1 yields a non periodic signal: | ||
| + | |||
| + | [[Image:HW2A2_ECE301Fall2008mboutin.png]] | ||
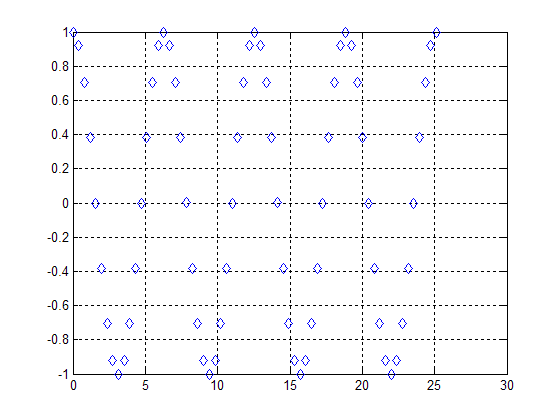
Sampling at a frequency of .125*pi yields a periodic signal: | Sampling at a frequency of .125*pi yields a periodic signal: | ||
| + | |||
| + | [[Image:HW2A3_ECE301Fall2008mboutin.png]] | ||
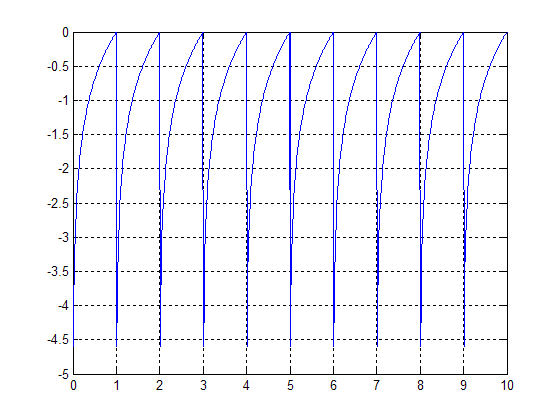
Taking a non periodic signal x(t)=log(t)and making it periodic can be done by taking a portion of the signal and repeating it over and over. | Taking a non periodic signal x(t)=log(t)and making it periodic can be done by taking a portion of the signal and repeating it over and over. | ||
| + | |||
| + | [[Image:HW2A4_ECE301Fall2008mboutin.png]] | ||
<pre> | <pre> | ||
Latest revision as of 08:38, 11 September 2008
Periodic Signals
The signal x(t)=sin(t) was chosen:
Sampling at a frequency of 1 yields a non periodic signal:
Sampling at a frequency of .125*pi yields a periodic signal:
Taking a non periodic signal x(t)=log(t)and making it periodic can be done by taking a portion of the signal and repeating it over and over.
clc
clear
t=.01:.01:1;
x=log(t);
i=[];
for d=1:10
i=[i,x];
end
t=[.01:.01:10];
plot(t,i)
grid on