(→Question 1) |
(→Question 1) |
||
| Line 5: | Line 5: | ||
Recall that this signal is periodic if <math>T = {\omega_0\over2\pi}\,</math> is rational. | Recall that this signal is periodic if <math>T = {\omega_0\over2\pi}\,</math> is rational. | ||
| − | Say I choose the sampling frequency <math> | + | Say I choose the sampling frequency <math>T_s=.1\,</math> |
The output will be: | The output will be: | ||
| Line 11: | Line 11: | ||
[[Image:Smooth_sin_ECE301Fall2008mboutin.jpg]] | [[Image:Smooth_sin_ECE301Fall2008mboutin.jpg]] | ||
| − | But if I choose the sampling frequency to be <math> | + | But if I choose the sampling frequency to be <math>T_s=.7\,</math> |
[[Image:Messed_sin_ECE301Fall2008mboutin.jpg]] | [[Image:Messed_sin_ECE301Fall2008mboutin.jpg]] | ||
Revision as of 08:21, 11 September 2008
Question 1
I chose the signal $ x[n]=e^{j\pi n} \, $ which Jeff Kubascik posted on his HW1.
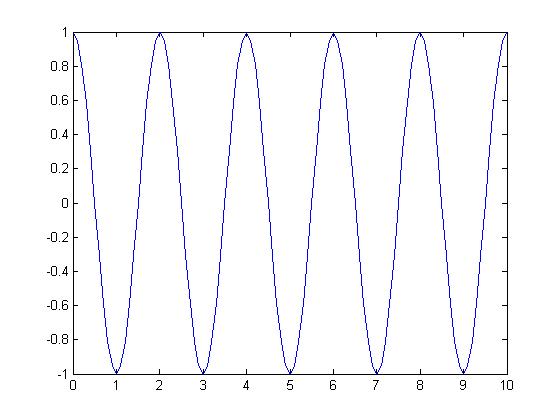
Recall that this signal is periodic if $ T = {\omega_0\over2\pi}\, $ is rational.
Say I choose the sampling frequency $ T_s=.1\, $
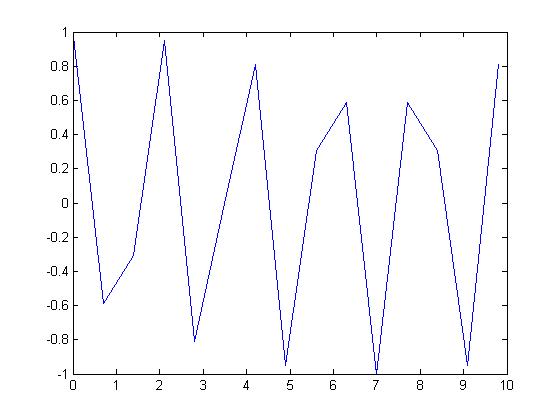
The output will be:
But if I choose the sampling frequency to be $ T_s=.7\, $