(→Part C: Linearity) |
(→Part C: Linearity) |
||
| Line 12: | Line 12: | ||
Path Two: | Path Two: | ||
[[Image:Partc2_ECE301Fall2008mboutin.JPG]] | [[Image:Partc2_ECE301Fall2008mboutin.JPG]] | ||
| + | |||
| + | |||
| + | |||
| + | === Example of a Linear System === | ||
| + | |||
| + | For this example, we take <math> x</math><sub>1</sub><math>(t) = x </math> and <math> x</math><sub>2</sub><math>(t) = 0 </math>. We will also take <math> a = 1 </math> and <math> b = 5 </math>. Taking the "first path" produces a result of <math> z</math><sub>1</sub><math>(t) = 1*x^2 +5*0</math>, while taking the "second path" produces a result of <math> z</math><sub></sub><math>(t) = (1*x + 0*5)^2 = x^2 </math>. Because <math>z</math><sub>1</sub><math>(t)</math> = <math>z</math><sub>2</sub><math>(t)</math>, the system is linear. | ||
Revision as of 14:51, 10 September 2008
Part C: Linearity
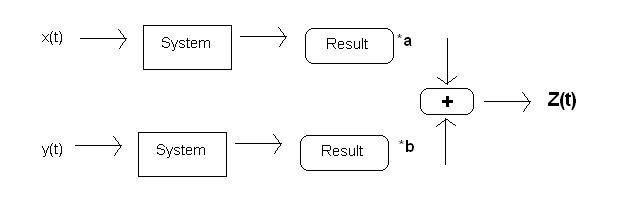
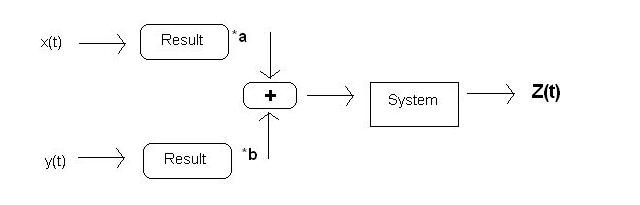
A linear system is a system such that for any constants $ a $ and $ b $ on the complex plane, inputs $ x(t) $ and $ y(t) $ produce the same $ z(t) $ no matter which of the following two paths they take through the system:
Example of a Linear System
For this example, we take $ x $1$ (t) = x $ and $ x $2$ (t) = 0 $. We will also take $ a = 1 $ and $ b = 5 $. Taking the "first path" produces a result of $ z $1$ (t) = 1*x^2 +5*0 $, while taking the "second path" produces a result of $ z $$ (t) = (1*x + 0*5)^2 = x^2 $. Because $ z $1$ (t) $ = $ z $2$ (t) $, the system is linear.