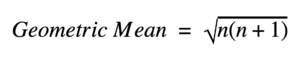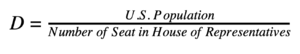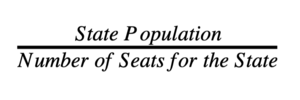| Line 10: | Line 10: | ||
Jefferson’s method is similar to Hamilton’s method, but includes an additional variable d to lower the value of the denominator for the State Quota and raise the quota [Cau10]: | Jefferson’s method is similar to Hamilton’s method, but includes an additional variable d to lower the value of the denominator for the State Quota and raise the quota [Cau10]: | ||
| − | + | [[File:Topic12Background2.png|300x140px|thumbnail|left]] | |
In this procedure, the value of d is such that when the State Quotas are rounded down they add to the correct number of House seats. This method was deemed constitutional and was used until 1842. | In this procedure, the value of d is such that when the State Quotas are rounded down they add to the correct number of House seats. This method was deemed constitutional and was used until 1842. | ||
| Line 17: | Line 17: | ||
The Huntington-Hill procedure is, again, similar to the Hamilton method [Cau10, 41]: | The Huntington-Hill procedure is, again, similar to the Hamilton method [Cau10, 41]: | ||
| − | + | [[File:Topic12Background3.png|300x140px|thumbnail|left]] | |
However, rather than simply rounding down to determine the State Quota, the procedure uses the geometric mean. To do this, round the State Quota down and call this number n. Then, compare this number to the geometric mean of n and n+1: | However, rather than simply rounding down to determine the State Quota, the procedure uses the geometric mean. To do this, round the State Quota down and call this number n. Then, compare this number to the geometric mean of n and n+1: | ||
| − | + | [[File:Topic12Background4.png|300x140px|thumbnail|left]] | |
If the State Quota is greater than the calculated geometric mean, allocate that state n+1 seats. In all other cases, give the state n seats. As in the Webster method, D must be adjusted such that the total number of seats to apportion match the number of seats available. The Huntington-Hill method tends to favor small states, as the rounding is on a geometric mean and thus favors smaller quotas. Smaller quotas are more desirable for smaller states because it means these States can qualify to have the same number of Representatives with few residents in their State. (For examples of Huntington-Hill’s method and the previous methods of apportionment mentioned earlier, refer to this resource from the U.S. Census Bureau [Bur17]). The Huntington-Hill method in particular was recently challenged in two U.S. District Court cases: Montana v. U.S. Department of Commerce (U.S. District Court, 1991) and Montana v. U.S. Department of Commerce (U.S. District Court, 1992). | If the State Quota is greater than the calculated geometric mean, allocate that state n+1 seats. In all other cases, give the state n seats. As in the Webster method, D must be adjusted such that the total number of seats to apportion match the number of seats available. The Huntington-Hill method tends to favor small states, as the rounding is on a geometric mean and thus favors smaller quotas. Smaller quotas are more desirable for smaller states because it means these States can qualify to have the same number of Representatives with few residents in their State. (For examples of Huntington-Hill’s method and the previous methods of apportionment mentioned earlier, refer to this resource from the U.S. Census Bureau [Bur17]). The Huntington-Hill method in particular was recently challenged in two U.S. District Court cases: Montana v. U.S. Department of Commerce (U.S. District Court, 1991) and Montana v. U.S. Department of Commerce (U.S. District Court, 1992). | ||
| Line 29: | Line 29: | ||
The Dean method was proposed as an alternative method of apportionment to the Huntington-Hill method. This method uses the same definition of D as previous methods [Cau10]: | The Dean method was proposed as an alternative method of apportionment to the Huntington-Hill method. This method uses the same definition of D as previous methods [Cau10]: | ||
| − | + | [[File:Topic12Background5.png|300x140px|thumbnail|left]] | |
However, each state obtains the number of seats such that: | However, each state obtains the number of seats such that: | ||
| − | + | [[File:Topic12Background6.png|300x140px|thumbnail|left]] | |
Is as close to the value of D as possible where D can be adjusted until the predetermined size of the House of Representatives is equal to the total number of seats apportioned. If the apportionment process had used Dean’s method rather than Huntington-Hill’s method, Montana would have kept its two seats in the House and the State of Washington would have lost a seat instead as demonstrated in Tables 1 and 2. For this reason, Montana advocated for the Dean’s method in their suit. Yet, in the end the courts ruled that the use of the Huntington-Hill method was, in fact, constitutional. For more background information regarding the rationale behind these court cases, please refer to [92b]. | Is as close to the value of D as possible where D can be adjusted until the predetermined size of the House of Representatives is equal to the total number of seats apportioned. If the apportionment process had used Dean’s method rather than Huntington-Hill’s method, Montana would have kept its two seats in the House and the State of Washington would have lost a seat instead as demonstrated in Tables 1 and 2. For this reason, Montana advocated for the Dean’s method in their suit. Yet, in the end the courts ruled that the use of the Huntington-Hill method was, in fact, constitutional. For more background information regarding the rationale behind these court cases, please refer to [92b]. | ||
| Line 39: | Line 39: | ||
''Table 1: The absolute and relative differences between the actual average district size and the ideal district size in an apportionment using the '''Huntington-Hill Method''' (Montana has one Representative, and Washington has nine Representatives) [92b] | ''Table 1: The absolute and relative differences between the actual average district size and the ideal district size in an apportionment using the '''Huntington-Hill Method''' (Montana has one Representative, and Washington has nine Representatives) [92b] | ||
'' | '' | ||
| − | + | ||
| + | [[File:Topic12Background7.png|thumbnail|center]] | ||
"Table 2: The absolute and relative differences between the actual average district size and the ideal district size in an apportionment using the '''Dean Method''' (Montana has two Representatives, and Washington has eight Representatives) [92b]" | "Table 2: The absolute and relative differences between the actual average district size and the ideal district size in an apportionment using the '''Dean Method''' (Montana has two Representatives, and Washington has eight Representatives) [92b]" | ||
| − | + | [[File:Topic12Background8.png|thumbnail|center]] | |
[[Category:Walther_MA279_Fall2018_topic12| Return to Main Topic Page]] | [[Category:Walther_MA279_Fall2018_topic12| Return to Main Topic Page]] | ||
[[Category:MA279Fall2018Walther | Return to MA279 Course Page]] | [[Category:MA279Fall2018Walther | Return to MA279 Course Page]] | ||
Revision as of 21:56, 2 December 2018
Background on Montana challenging the Huntington-Hill method
One of the important functions of the United States Census is that the information from these census reports helps State legislators and governors in Congressional redistricting. Every ten years after the results of the U.S. Census are released, lawmakers must use this information to calculate how many representatives in the House of Representatives each state obtains based on state population size. However, the method used to determine Congressional apportionment has changed several times throughout U.S. history. After the first U.S. Census in 1790, Congress attempted to pass the first apportionment bill using the Hamilton method [92a]. This method sets each State Quota, or number of representatives using the following procedure [Cau10]:
D is an important variable in all apportionment calculations as it represents the ratio of U.S. residents to Representatives. The quotas are rounded down and after all state quotas have been calculated the remaining seats are allocated to states with the highest remainders in the State Quota. However, this bill was vetoed by President George Washington. Washington viewed the use of Alexander Hamilton’s method for apportionment as unconstitutional. This is because Hamilton’s method does not have a uniform divisor when determining the number of representatives and would allow some states to have more than one representative for every thirty thousand citizens, which violates Article 1 Section II of the Constitution [92a]. Thus, the the bill was revised to use a new method proposed by Thomas Jefferson. This bill became known as the Apportionment Act of 1792.
Jefferson’s method is similar to Hamilton’s method, but includes an additional variable d to lower the value of the denominator for the State Quota and raise the quota [Cau10]:
In this procedure, the value of d is such that when the State Quotas are rounded down they add to the correct number of House seats. This method was deemed constitutional and was used until 1842. After the 1840 Census, Congress changed to the Webster method of apportionment whose procedure follows is the same as Hamilton’s method, but instead of rounding the State Quotas down, remainders that have fraction of 0.50 and above are given an additional seat [91]. The divisor D is adjusted as needed apportioned all seats available. Nevertheless, the method changed again to the Hamilton method in 1850, back to Webster’s method in 1911, and finally to the Huntington-Hill method that is currently used.
The Huntington-Hill procedure is, again, similar to the Hamilton method [Cau10, 41]:
However, rather than simply rounding down to determine the State Quota, the procedure uses the geometric mean. To do this, round the State Quota down and call this number n. Then, compare this number to the geometric mean of n and n+1:
If the State Quota is greater than the calculated geometric mean, allocate that state n+1 seats. In all other cases, give the state n seats. As in the Webster method, D must be adjusted such that the total number of seats to apportion match the number of seats available. The Huntington-Hill method tends to favor small states, as the rounding is on a geometric mean and thus favors smaller quotas. Smaller quotas are more desirable for smaller states because it means these States can qualify to have the same number of Representatives with few residents in their State. (For examples of Huntington-Hill’s method and the previous methods of apportionment mentioned earlier, refer to this resource from the U.S. Census Bureau [Bur17]). The Huntington-Hill method in particular was recently challenged in two U.S. District Court cases: Montana v. U.S. Department of Commerce (U.S. District Court, 1991) and Montana v. U.S. Department of Commerce (U.S. District Court, 1992).
Using the Huntington-Hill method with the 1990 U.S. Census results, the reapportionment of representatives determined that 8 states would gain a total of 19 additional seats and 13 States would lose a total of 19 seats [92b]. One of the States that lost a seat from this apportionment was Montana. The loss of one seat was significant for Montana because before the reapportionment, Montana had only two seats in the House of Representatives; thus, their delegation was essentially halved. In response, Montana Senators, Representatives, its Governor, Attorney General, and Secretary of State filed suit against the federal government, insisting that Montana was entitled to two seats. They claimed that the existing apportionment method violated Article I, Section 2 of the Constitution, which mandates that apportionment should have the greatest possible equality in the number of individuals per seat in the House of Representatives.
The Dean method was proposed as an alternative method of apportionment to the Huntington-Hill method. This method uses the same definition of D as previous methods [Cau10]:
However, each state obtains the number of seats such that:
Is as close to the value of D as possible where D can be adjusted until the predetermined size of the House of Representatives is equal to the total number of seats apportioned. If the apportionment process had used Dean’s method rather than Huntington-Hill’s method, Montana would have kept its two seats in the House and the State of Washington would have lost a seat instead as demonstrated in Tables 1 and 2. For this reason, Montana advocated for the Dean’s method in their suit. Yet, in the end the courts ruled that the use of the Huntington-Hill method was, in fact, constitutional. For more background information regarding the rationale behind these court cases, please refer to [92b].
Table 1: The absolute and relative differences between the actual average district size and the ideal district size in an apportionment using the Huntington-Hill Method (Montana has one Representative, and Washington has nine Representatives) [92b]
"Table 2: The absolute and relative differences between the actual average district size and the ideal district size in an apportionment using the Dean Method (Montana has two Representatives, and Washington has eight Representatives) [92b]"