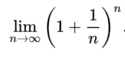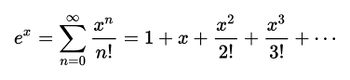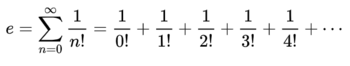| Line 20: | Line 20: | ||
|} | |} | ||
As can be seen from the table, the value of the formula converges towards a constant number, which in this case is ''e''. Therefore, we can see that Bernoulli's formula is one way to calculate the value of ''e''. <br /><br /> | As can be seen from the table, the value of the formula converges towards a constant number, which in this case is ''e''. Therefore, we can see that Bernoulli's formula is one way to calculate the value of ''e''. <br /><br /> | ||
| − | Leonhard Euler was the one who defined this constant with the symbol ''e'' in one of his papers in 1731. | + | Leonhard Euler was the one who defined this constant with the symbol ''e'' in one of his papers in 1731. The agreed upon theory is that he named the number ''e'' not after himself but because it was the next letter in the variables he was using. Euler found a continuous fractional expansion for ''e'' that was never ending: |
| + | [[File: Econtinous.png|300px|thumbnail]] | ||
| + | This never ending continuous fraction was the first proof for the irrationality of the number. <br /> <br /> | ||
| + | He was also able to find the first 18 digits of ''e'' using a different formula he came up with to define the number. This particular formula is based on the Taylor Series of ''e<sup>x</sup>''. The Taylor Series of ''e<sup>x</sup>'' is: | ||
[[File:Extaylor.jpg|350px|thumbnail]] | [[File:Extaylor.jpg|350px|thumbnail]] | ||
Since ''e'' is the same as taking ''x=1'' in the series, we get the following formula for ''e'': | Since ''e'' is the same as taking ''x=1'' in the series, we get the following formula for ''e'': | ||
[[File:Eseries.png|350px|thumbnail]] | [[File:Eseries.png|350px|thumbnail]] | ||
| − | Therefore, we can see another way of calculating the value of ''e''. Bernoulli's formula is more | + | Therefore, we can see another way of calculating the value of ''e''. Typically, using Bernoulli's formula is more tedious since taking powers of irrational numbers can get complicated quickly. But Euler's formula is much simpler since it uses relatively common fractions and addition to find the value. |
| + | |||
| + | '''References''' <br /> | ||
| + | Maor, E. (1994). ''E: The Story of a Number.'' Princeton, NJ: Princeton University Press. Retrieved from http://webwork.utleon.edu.mx/Paginas/Libros/E%20-%20The%20Story%20of%20a%20Number.pdf <br /> | ||
| + | Haran, B. [Numberphile]. (2016, December 19). ''e (Euler's Number) - Numberphile'' [Video File]. Retrieved from https://youtu.be/AuA2EAgAegE <br /> | ||
| + | Sýkora, S. (2008, March 31). Mathematical Constants and Sequences. In ''Mathematical Constants and Sequences''. Retrieved from http://www.ebyte.it/library/educards/constants/MathConstants.html <br /> | ||
| + | O'Connor, J. J., & Robertson, E. F. (2001, September). The number e. Retrieved from http://www-history.mcs.st-and.ac.uk/HistTopics/e.html <br /> | ||
| + | Sandifer, E. (2006, February). How Euler Did It. Retrieved from http://eulerarchive.maa.org/hedi/HEDI-2006-02.pdf | ||
[[Category:MA279Fall2018Walther]] | [[Category:MA279Fall2018Walther]] | ||
Revision as of 23:48, 1 December 2018
Defining e
There are a number of constants in mathematics that are defined by geometry in some way. For example, Archimedes' constant π is defined as the ratio between the circumference and diameter of a circle. Pythagoras' constant sqrt(2) is defined as the length of the diagonal of a square with sides of 1. However, e is based on formulae rather than geometry.
When Jacob Bernoulli was studying compound interest in 1683, his work led him to a formula:
Let's observe what happens to the value of the formula when different values of n are used:
| n | (1+1/n)^n |
|---|---|
| 5 | 2.48832 |
| 50 | 2.69159 |
| 100 | 2.70481 |
| 100,000 | 2.71827 |
| 1,000,000 | 2.71828 |
As can be seen from the table, the value of the formula converges towards a constant number, which in this case is e. Therefore, we can see that Bernoulli's formula is one way to calculate the value of e.
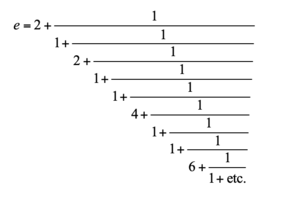
Leonhard Euler was the one who defined this constant with the symbol e in one of his papers in 1731. The agreed upon theory is that he named the number e not after himself but because it was the next letter in the variables he was using. Euler found a continuous fractional expansion for e that was never ending:
This never ending continuous fraction was the first proof for the irrationality of the number.
He was also able to find the first 18 digits of e using a different formula he came up with to define the number. This particular formula is based on the Taylor Series of ex. The Taylor Series of ex is:
Since e is the same as taking x=1 in the series, we get the following formula for e:
Therefore, we can see another way of calculating the value of e. Typically, using Bernoulli's formula is more tedious since taking powers of irrational numbers can get complicated quickly. But Euler's formula is much simpler since it uses relatively common fractions and addition to find the value.
References
Maor, E. (1994). E: The Story of a Number. Princeton, NJ: Princeton University Press. Retrieved from http://webwork.utleon.edu.mx/Paginas/Libros/E%20-%20The%20Story%20of%20a%20Number.pdf
Haran, B. [Numberphile]. (2016, December 19). e (Euler's Number) - Numberphile [Video File]. Retrieved from https://youtu.be/AuA2EAgAegE
Sýkora, S. (2008, March 31). Mathematical Constants and Sequences. In Mathematical Constants and Sequences. Retrieved from http://www.ebyte.it/library/educards/constants/MathConstants.html
O'Connor, J. J., & Robertson, E. F. (2001, September). The number e. Retrieved from http://www-history.mcs.st-and.ac.uk/HistTopics/e.html
Sandifer, E. (2006, February). How Euler Did It. Retrieved from http://eulerarchive.maa.org/hedi/HEDI-2006-02.pdf