| Line 64: | Line 64: | ||
=== Graph Coloring === | === Graph Coloring === | ||
| − | Graph coloring is nothing but a simple way of labeling graph components such as vertices, edges, and regions under some constraints. For our problem, we will be considering the vertex coloring variation where no two adjacent vertices are colored with | + | Graph coloring is nothing but a simple way of labeling graph components such as vertices, edges, and regions under some constraints. For our problem, we will be considering the vertex coloring variation where no two adjacent vertices are colored with the same color. This minimum number of colors that must be used is called the chromatic number. The ''k-coloring'' of the graph is an assignment of colors to each vertex that meets the above constraints and uses exactly k distinct colors in the coloring. Finding the minimum value of k such that a coloring exist is the problem of interest to us. |
=== Reducing Scheduling to Graph Coloring === | === Reducing Scheduling to Graph Coloring === | ||
Revision as of 18:29, 29 November 2018
Contents
U.S. Senate Committee Meetings Scheduling
The United States of America Senate has 16 standing senate committees which meet on a regular basis. These meeting are extremely important as legislation that gets passed in the Senate often originates in these meetings. Each committee is composed of a collection of senate members with the possibility of overlapping members between the committees. Scheduling these meetings in an efficient manner so that we don’t waste time of the committee members is an important problem that needs to be solved. The optimal solution to this problem will be obtained by scheduling multiple meetings within the same time frame, constrained on having no overlapping members between any two concurrent meetings.
Currently, the nation's 16 committees consists of the following sectors:
- Agriculture, Nutrition, and Forestry
- Appropriations
- Armed Services
- Banking, Housing, and Urban Affairs
- Budget
- Commerce, Science, and Transportation
- Energy and Natural Resources
- Environment and Public Works
- Finance
- Foreign Relations
- Health, Education, Labor, and Pensions
- Homeland Security and Governmental Affairs
- Judiciary
- Rules and Administration
- Small Business and Entrepreneurship
- Veterans' Affairs
Committee Overlaps
Out of the 16 committees there are a total of $ \textstyle\binom {16}2 $= 120 possible committee intersections, i.e. a pair of committees with one or more members belonging to both committees. Thus, these parties cannot hold simultaneous meetings. The current US senate memberships results in a total of 110 committee intersections. The pairs of congressional senates that have no intersections are:
| Committee I | Committee II |
|---|---|
| Agriculture, Nutrition, and Forestry | Foreign Relations |
| Appropriations | Finance |
| Armed Services | Energy and Natural Resources |
| Banking, Housing, and Urban Affairs | Energy and Natural Resources |
| Budget | Energy and Natural Resources |
| Environment and Public Works | Health, Education, Labor, and Pensions |
| Homeland Security and Governmental Affairs | Rules and Administration |
| Homeland Security and Governmental Affairs | Veterans' Affairs |
| Rules and Administration | Small Business and Entrepreneurship |
| Rules and Administration | Veterans' Affairs |
Problem Formulation
The goal of the problem is to minimize the time frame within which all the committees can conduct their meeting. Any intersection between two committees forces the two committees to hold meetings at different time slots. This problem is fairly common, and can be reduced into an Undirected Graph problem called the K-Graph Coloring problem.
Graph Coloring
Graph coloring is nothing but a simple way of labeling graph components such as vertices, edges, and regions under some constraints. For our problem, we will be considering the vertex coloring variation where no two adjacent vertices are colored with the same color. This minimum number of colors that must be used is called the chromatic number. The k-coloring of the graph is an assignment of colors to each vertex that meets the above constraints and uses exactly k distinct colors in the coloring. Finding the minimum value of k such that a coloring exist is the problem of interest to us.
Reducing Scheduling to Graph Coloring
The senate committee scheduling problem can be reduced to such a graph coloring problem in the following manner. We construct a graph G with the following properties:
- Each committee is a vertex.
A* n edge is placed between two vertices if the corresponding committees share a member. We can note that if there exists a k-coloring of this graph, the committee meetings can be scheduled using k time slots. We can simply assign each time slot a color and since each vertex is colored, we get a time slot for each vertex i.e. committee. There can be no conflicts as if any two committees have the same time slot (color), they will not have any common members otherwise there would be an edge between the vertices and by the restriction, the coloring is not valid.
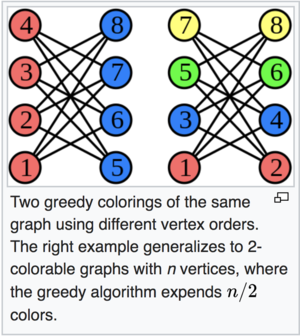
Now, we need to find the minimum k. The importance of finding the minimum is shown below in the figure:
This left image is a 2-coloring of the graph while the right image is a 4-coloring of the same graph. Now, if we interpret the graph in the context of our problem, the 2-coloring uses 2 time slots while the right uses 4. In the 4-coloring, while committees 1 and 2 are in a meeting at a time slot red, the remaining committees are sitting idle which is a waste of senator’s time. Scheduling as many meetings as possible in parallel is the goal. Hence, we want to find the minimum value k can take for out committee graph.
Algorithms
The vertex coloring problem is NP-complete. It can be shown by reducing the 3SAT problem to this problem. This means that there is no known polynomial time algorithm for this problem.
Brute-force search for a k-coloring considers each of the kn assignments of k colors to n vertices and checks for each if it is legal. To compute the chromatic number and the chromatic polynomial, this procedure is used for every k=1, …, n-1, impractical for all but the smallest input graphs. In our case of 16 committees, the worst case is if every member is on every committee, which means we would run our algorithm on all values of k from 1 to 16. This would mean in the worst case looking at different colorings which is computationally intractable. We can see that for larger values than 16, this value increases very fast.
We can improve upon this naïve method using backtracking. We assign each vertex a color that does not clash with any of its neighboring vertex’s color and repeat the process until we either finish coloring all vertices or have no valid colors left to assign. This avoids looking at coloring where there is more than one point of conflict significantly improving the run time. This method is still exponentially slow in the worst case and even after several heuristics and optimizations, it is still intractable for large graphs. For the purposes of our problems, however, this method is feasible.
References
Description of Graphs: https://en.wikipedia.org/wiki/Graph_(abstract_data_type)
Graph Coloring: https://en.wikipedia.org/wiki/Graph_coloring
Senate Committees: https://www.senate.gov/pagelayout/committees/d_three_sections_with_teasers/committees_home.htm
Welsh Powell Algorithm: http://graphstream-project.org/doc/Algorithms/Welsh-Powell/
NP - Completeness intro: https://www.geeksforgeeks.org/np-completeness-set-1/
Graph Coloring implementation: https://github.com/MUSoC/Visualization-of-popular-algorithms-in-Python/tree/master/Graph%20Coloring