| Line 6: | Line 6: | ||
<math>\bar{p} = q\bar{d}</math> | <math>\bar{p} = q\bar{d}</math> | ||
| + | |||
<math>V_1 - V_2 = -\int_1^2\bar{E}\cdot d\bar{l} = 10,000\hspace{2cm} D= \epsilon\bar{E} = \epsilon_0\bar{E} + \bar{p}</math> | <math>V_1 - V_2 = -\int_1^2\bar{E}\cdot d\bar{l} = 10,000\hspace{2cm} D= \epsilon\bar{E} = \epsilon_0\bar{E} + \bar{p}</math> | ||
| + | |||
<math>-E_zl = 10,000</math> | <math>-E_zl = 10,000</math> | ||
| + | |||
<math>\bar{E} = - \frac{10,000}{l}\hat{z}</math> | <math>\bar{E} = - \frac{10,000}{l}\hat{z}</math> | ||
| + | |||
<math>\bar{F} = - \frac{10,000q}{l}\hat{z} </math> | <math>\bar{F} = - \frac{10,000q}{l}\hat{z} </math> | ||
------------------------------------------------------------------------------------ | ------------------------------------------------------------------------------------ | ||
| Line 14: | Line 18: | ||
2) | 2) | ||
| − | [[Image: | + | [[Image:A2FO32013.png|Alt text|550x232px]] |
<math>P = VI = I^2R = \frac{V^2}{R}</math> | <math>P = VI = I^2R = \frac{V^2}{R}</math> | ||
| + | |||
<math>F = q(\bar{E} + \bar{\mu} \times\bar{B} ) = 0</math> | <math>F = q(\bar{E} + \bar{\mu} \times\bar{B} ) = 0</math> | ||
| + | |||
<math>\bar{E} = \frac{-\bar{\mu}\times\bar{B}}{q} = \frac{-\bar{v}\times\bar{B}}{q}\leftarrow\hat{z}</math> | <math>\bar{E} = \frac{-\bar{\mu}\times\bar{B}}{q} = \frac{-\bar{v}\times\bar{B}}{q}\leftarrow\hat{z}</math> | ||
| + | |||
<math>\nabla\times\bar{H} = j\omega\epsilon\bar{E}+\bar{J}</math> | <math>\nabla\times\bar{H} = j\omega\epsilon\bar{E}+\bar{J}</math> | ||
| + | |||
<math>V_1 - V_2 = -\int_1^2\bar{E}\cdot d\bar{l} = \frac{-d}{q}|\bar{v}\times\bar{B}|^2</math> | <math>V_1 - V_2 = -\int_1^2\bar{E}\cdot d\bar{l} = \frac{-d}{q}|\bar{v}\times\bar{B}|^2</math> | ||
| + | |||
<math>p = \frac{d^2}{q^2}|\bar{v}\times\bar{B}|</math> | <math>p = \frac{d^2}{q^2}|\bar{v}\times\bar{B}|</math> | ||
Revision as of 15:49, 17 June 2017
1)
$ F = q (\bar{E} + \cancelto{0}{\bar{\mu}\times\bar{B}} ) = qE $
$ \bar{p} = q\bar{d} $
$ V_1 - V_2 = -\int_1^2\bar{E}\cdot d\bar{l} = 10,000\hspace{2cm} D= \epsilon\bar{E} = \epsilon_0\bar{E} + \bar{p} $
$ -E_zl = 10,000 $
$ \bar{E} = - \frac{10,000}{l}\hat{z} $
$ \bar{F} = - \frac{10,000q}{l}\hat{z} $
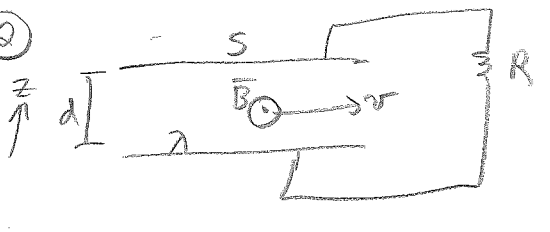
\\ 2)
$ P = VI = I^2R = \frac{V^2}{R} $
$ F = q(\bar{E} + \bar{\mu} \times\bar{B} ) = 0 $
$ \bar{E} = \frac{-\bar{\mu}\times\bar{B}}{q} = \frac{-\bar{v}\times\bar{B}}{q}\leftarrow\hat{z} $
$ \nabla\times\bar{H} = j\omega\epsilon\bar{E}+\bar{J} $
$ V_1 - V_2 = -\int_1^2\bar{E}\cdot d\bar{l} = \frac{-d}{q}|\bar{v}\times\bar{B}|^2 $
$ p = \frac{d^2}{q^2}|\bar{v}\times\bar{B}| $