(→Periodic Signal) |
|||
| Line 11: | Line 11: | ||
tan(t) = tan(t + T) for some value of T > 0 | tan(t) = tan(t + T) for some value of T > 0 | ||
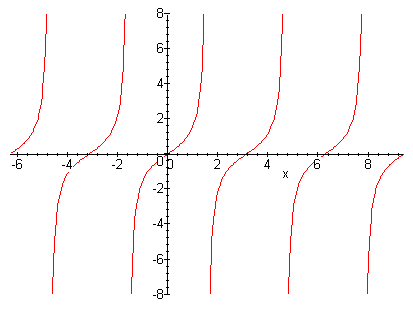
| − | Since we know that tan(t) repeats itself after every period of <math> t = \pi</math> , we know that x(t) is a periodic signal. | + | Since we know that tan(t) repeats itself after every period of <math> t = \pi</math> , we know that x(t) is a periodic signal. |
| + | |||
| + | [[Image:Tangent_ECE301Fall2008mboutin.gif]] | ||
==Non Periodic Signal== | ==Non Periodic Signal== | ||
Revision as of 07:47, 4 September 2008
A discrete time signal is periodic if there exists T > 0 such that x(t + T) = x(t)
A continuous time signal is periodic if there exists some integer N > 0 such that x[n + N] = x[n]
Periodic Signal
Let $ x(t) = tan(t) $
For x(t) to be periodic, the following must hold true:
tan(t) = tan(t + T) for some value of T > 0
Since we know that tan(t) repeats itself after every period of $ t = \pi $ , we know that x(t) is a periodic signal.
Non Periodic Signal
Let $ x[n] = e^{jn} $
For x[n] to be periodic, the following must hold true:
$ e^{jn} = e^{j(n+N)} $ for some integer N
$ e^{jn} = e^{jn} e^{jN} $
$ 1 = e^{jN} $
1 = cos(N) + jsin(N)
This equation only holds true if $ N = 2\pi $ or some multiple of $ 2\pi $
Therefore$ x[n] = e^{jn} $ is not periodic because $ 2\pi $ is not an integer.