(Finished Statement of Theorem) |
(Images added) |
||
| Line 24: | Line 24: | ||
Using the Nyquist condition to set the sampling period <math>T</math>:<br><math>\frac{1}{T} > 2f_M \ or \ T < \frac{1}{f_s}</math> | Using the Nyquist condition to set the sampling period <math>T</math>:<br><math>\frac{1}{T} > 2f_M \ or \ T < \frac{1}{f_s}</math> | ||
| + | |||
| + | ---- | ||
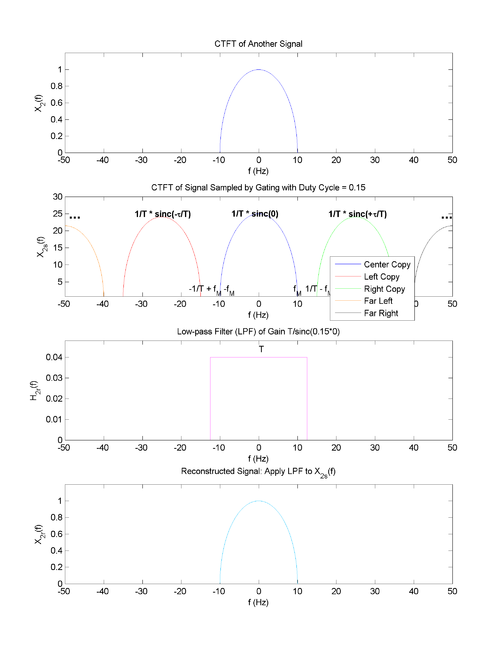
| + | ==Simple Example: Frequency Domain== | ||
| + | [[Image:Nyquist_slecture_1.png|500px|center|border|Figure 1: Simple Example in Frequency Domain]] | ||
| + | |||
| + | ---- | ||
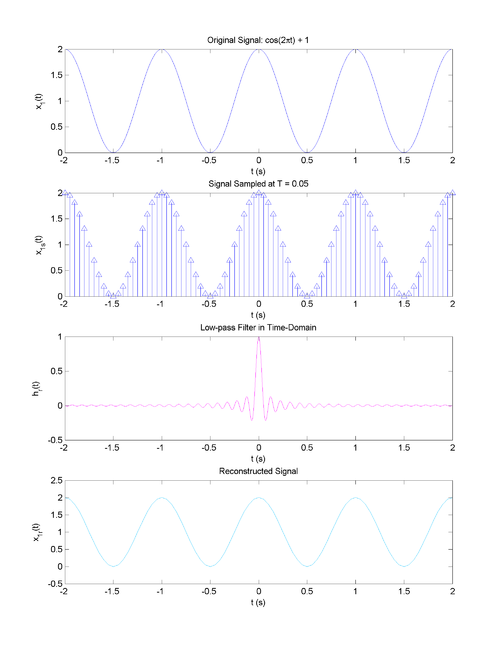
| + | ==Simple Example: Time Domain and Whitaker-Kotelnikov-Shannon Reconstruction== | ||
| + | [[Image:Nyquist_slecture_2.png|500px|center|border|Figure 2: Simple Example in Time Domain]] | ||
| + | |||
| + | ---- | ||
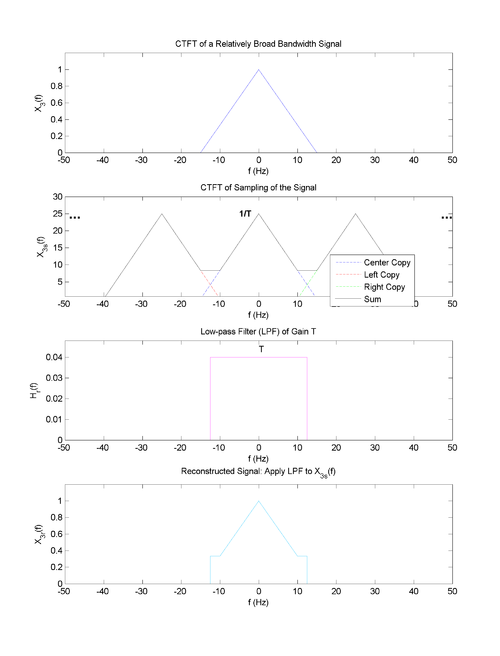
| + | ==More Complicated Example== | ||
| + | [[Image:Nyquist_slecture_3.png|500px|center|border|Figure 3: More Complicated Example]] | ||
| + | |||
| + | --- | ||
| + | ==Nyquist Condition Violation Example== | ||
| + | [[Image:Nyquist_slecture_4.png|500px|center|border|Figure 4: Nyquist Condition Violation Example]] | ||
---- | ---- | ||
Revision as of 19:21, 5 October 2014
Nyquist Theorem
A slecture by ECE student Michael Hayashi
Partly based on the ECE438 Fall 2014 lecture material of Prof. Mireille Boutin.
Contents
Statement of Theorem
The Nyquist Theorem states that a signal may be perfectly reconstructed from its sampling provided that the original signal contains no frequency content above or equal to the sampling frequency. Applying mathematical expressions to the theorem, a signal $ x(t) $ may certainly be reconstructed perfectly from its sampling $ x_s(t) $if the continuous-time Fourier Transform (CTFT) of $ x(t) $ is zero for all magnitudes of frequency equal to or above half the sampling frequency (Nyquist condition).
Let the Nyquist sampling rate $ f_s $ be equal to this frequency of interest for reconstruction where $ f_M $ denotes the magnitude of the largest nonzero frequency in $ x(t) $:
$ f_s \triangleq 2f_M $
Nyquist condition:
$ X(f) = 0 \ \forall \ |f| \geq \frac{1}{2T} $
Using the Nyquist condition to set the sampling period $ T $:
$ \frac{1}{T} > 2f_M \ or \ T < \frac{1}{f_s} $
Simple Example: Frequency Domain
Simple Example: Time Domain and Whitaker-Kotelnikov-Shannon Reconstruction
More Complicated Example
---
Nyquist Condition Violation Example
Important Notes
- The Nyquist condition guarantees that the original signal may be reconstructed from the sampling, but there are signals that have CTFT's that allow for perfect reconstruction even when the Nyquist condition is violated.
- For signals with discontinuous CTFT magnitudes, $ f_s $ may be more clearly defined by stating that the Nyquist sampling rate is the least such frequency magnitude of $ X(f) $ for which $ X(f) = 0 $. This definition firmly places $ f_s $ outside any jumps to $ X(f) = 0 $.
- Restricting the Nyquist Theorem to purely real signals (the only physically producible signals) that have equal nonzero extent both in the positive-f and negative-f directions, the wording of the Nyquist condition may be relaxed to state that the CTFT of the original signal must not contain any frequencies equal to or higher than half the sampling frequency.
TO BE CONTINUED
Questions and comments
If you have any questions, comments, etc. please post them on this page.