| Line 53: | Line 53: | ||
---- | ---- | ||
| + | |||
1.1.2 Definition of Rep operator | 1.1.2 Definition of Rep operator | ||
| Line 60: | Line 61: | ||
---- | ---- | ||
| + | |||
1.1.3 Two representations of Rep operator | 1.1.3 Two representations of Rep operator | ||
| Line 65: | Line 67: | ||
<math>2.rep_{T}(x[t])=x(t) \ast P_{T}(T)</math> | <math>2.rep_{T}(x[t])=x(t) \ast P_{T}(T)</math> | ||
| − | |||
---- | ---- | ||
---- | ---- | ||
| + | |||
1.1.4 Relationship between two representation | 1.1.4 Relationship between two representation | ||
| Line 86: | Line 88: | ||
---- | ---- | ||
| + | |||
1.2.1 Introduction to Comb operator | 1.2.1 Introduction to Comb operator | ||
| Line 95: | Line 98: | ||
We can draw a conclusion from two figures above that x(t) is modulated by a impulse train with a period T. Just like putting a comb onto the signal and making it been 'sampled'. But this process is a little different from sampling. The continuous signal will become discrete after sampling while it will still be continuous after comb process. | We can draw a conclusion from two figures above that x(t) is modulated by a impulse train with a period T. Just like putting a comb onto the signal and making it been 'sampled'. But this process is a little different from sampling. The continuous signal will become discrete after sampling while it will still be continuous after comb process. | ||
| + | |||
| + | ---- | ||
| + | |||
| + | ---- | ||
| + | |||
| + | 1.2.2 Definition of Comb operator | ||
| + | |||
| + | Comb operator denote a process that 'sampling' a signal by using a impulse train with a specified period T. But the signal after this process will still be continuous. | ||
| + | |||
| + | ---- | ||
| + | |||
| + | ---- | ||
| + | 1.2.3 Two representations of Comb operator | ||
| + | |||
Revision as of 22:01, 12 September 2014
Definition of Rep and Comb
A slecture by ECE student Xiaozhe Fan
Partly based on the ECE438 Fall 2014 lecture material of Prof. Mireille Boutin.
1 Outline
1.1 Definition of Rep operator
1.1.1 Introduction to Rep operator
1.1.2 Definition of Rep operator
1.1.3 Two representations of Rep operator
1.1.4 Relationship between two representation
1.2 Definition of Comb operator
1.2.1 Introduction to Comb operator
1.2.2 Definition of Comb operator
1.2.3 Two representations of Comb operator
1.2.4 Relationship between two representation
1.1.1 Introduction to Rep operator
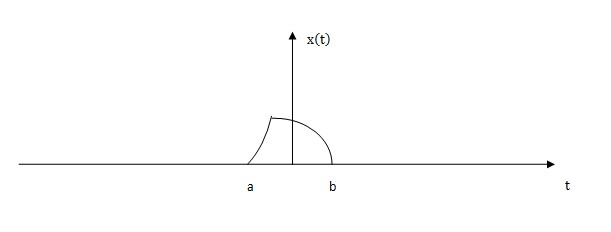
In order to understand Rep operator clearly, a graphical method is introduced as follows:
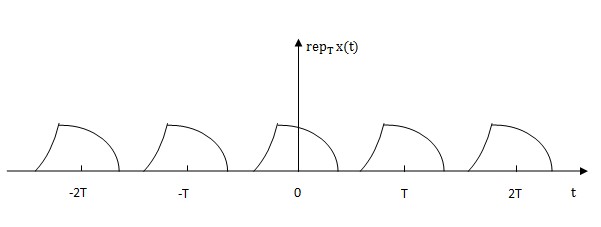
In the figure above, there is a little pulse with compact supports over a definite interval. When repeating it at capital T, We can get the following figure.
This process which is denoted by Rep operator have the same meaning as taking original function x(t) and shifting it by KT in which K∈N and -∞<K<+∞.
1.1.2 Definition of Rep operator
Rep operator denotes a kind of process which can periodically replicate a function with some specific period T. Where the function has a finite domain of argument and the minimum repeating period T has to > a+b(a denotes left boundary of the graph and b denotes right boundary of the graph ).
1.1.3 Two representations of Rep operator
$ 1.rep_{T}(x[t])=\sum_{k=-\infty}^{\infty}x(t-KT) $
$ 2.rep_{T}(x[t])=x(t) \ast P_{T}(T) $
1.1.4 Relationship between two representation
$ rep_{T}(x[t])=x(t) \ast P_{T}(T) \qquad \qquad \qquad Where \quad P_{T}(T)=\sum_{k=-\infty}^{\infty}\delta(t-KT) $
$ =x(t) \ast \sum_{k=-\infty}^{\infty}\delta(t-KT) $ $ =\int_{-\infty}^{\infty}x(\tau)\sum_{k=-\infty}^{\infty}\delta(t-KT-\tau)d\tau $ $ =\sum_{k=-\infty}^{\infty}\int_{-\infty}^{\infty}x(\tau)\delta(t-KT-\tau)d\tau $
$ Since \quad x(t)=\int_{-\infty}^{\infty}\delta(t-\tau)d\tau $
$ So \quad rep_{T}(x[t])=\sum_{k=-\infty}^{\infty}x(t-KT) $
We can transform the representation with convolution formula to another and vice versa.
1.2.1 Introduction to Comb operator
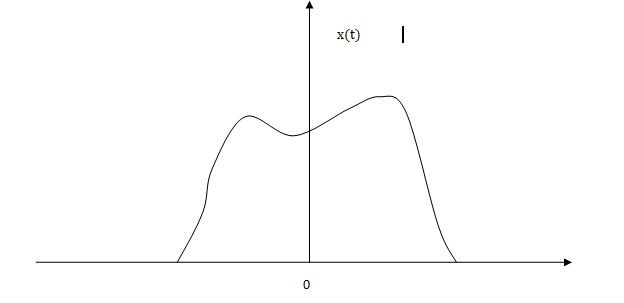
We just use the same method as the one we did previously.The graphical method is introduced as follows:
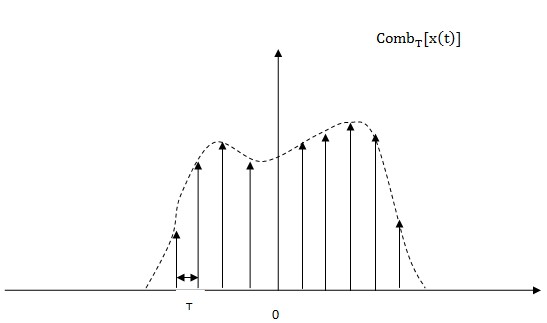
We can draw a conclusion from two figures above that x(t) is modulated by a impulse train with a period T. Just like putting a comb onto the signal and making it been 'sampled'. But this process is a little different from sampling. The continuous signal will become discrete after sampling while it will still be continuous after comb process.
1.2.2 Definition of Comb operator
Comb operator denote a process that 'sampling' a signal by using a impulse train with a specified period T. But the signal after this process will still be continuous.
1.2.3 Two representations of Comb operator
Post your slecture material here. Guidelines:
- If you wish to post your slecture anonymously, please contact your instructor to get an anonymous login. Otherwise, you will be identifiable through your Purdue CAREER account, and thus you will NOT be anonymous.
- Rephrase the material in your own way, in your own words, based on Prof. Boutin's lecture material.
- Feel free to add your own examples or your own material.
- Focus on the clarity of your explanation. It must be clear, easily understandable.
- Type text using wikitext markup language. Do not post a pdf. Do not upload a word file.
- Type all equations using latex code between <math> </math> tags.
- You may include graphs, pictures, animated graphics, etc.
- You may include links to other Project Rhea pages.
IMPORTANT: DO NOT PLAGIARIZE. If you use other material than Prof. Boutin's lecture material, you must cite your sources. Do not copy text word for word from another source; rephrase everything using your own words. Similarly for graphs, illustrations, pictures, etc. Make your own! Do not copy them from other sources.
(create a question page and put a link below)
Questions and comments
If you have any questions, comments, etc. please post them on this page.