| Line 3: | Line 3: | ||
Outline: | Outline: | ||
| − | |||
| − | |||
| − | + | = Email the group to see if anyone else is currently making changes before you begin making changes yourself!!!<br> = | |
| − | + | = P-groups = | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
'''Definitions:''' | '''Definitions:''' | ||
| Line 72: | Line 36: | ||
**A lie ring is a set R with two binary operations - addition and the Lie bracket - such that | **A lie ring is a set R with two binary operations - addition and the Lie bracket - such that | ||
***(R,+) is an abelian group; | ***(R,+) is an abelian group; | ||
| − | ***The bracket operation distributes over addition; | + | ***''Bilinearity:'' The bracket operation distributes over addition; |
| − | ***[x,x] = 0 for all x in R; | + | ***''Alternating on the vector space g:'' [x,x] = 0 for all x in R; |
| − | ***[[x,y],z]+[[y,z],x]+[[z,x],y]=0 for all x,y,z in R. | + | ***''The Jacobi Identity:'' [[x,y],z]+[[y,z],x]+[[z,x],y]=0 for all x,y,z in R. |
**If F is a field, and R is an F-vector space with a[x,y]=[ax,y] then R is a Lie algebra. | **If F is a field, and R is an F-vector space with a[x,y]=[ax,y] then R is a Lie algebra. | ||
**To every finite p-group one can associate a Lie ring L(G), and if G/G' is abelian then L(G) is actually a lie algebra over the finite field GF(p). | **To every finite p-group one can associate a Lie ring L(G), and if G/G' is abelian then L(G) is actually a lie algebra over the finite field GF(p). | ||
***Proposition: Let <span class="texhtml">φ</span> be an automorphism of the finite p-group G. Then <span class="texhtml">φ</span> induces an automorphism on L(G), and if <span class="texhtml">φ</span> has order prime to p, then the induced automorphism has the same order. | ***Proposition: Let <span class="texhtml">φ</span> be an automorphism of the finite p-group G. Then <span class="texhtml">φ</span> induces an automorphism on L(G), and if <span class="texhtml">φ</span> has order prime to p, then the induced automorphism has the same order. | ||
| + | |||
| + | |||
*Number of Groups | *Number of Groups | ||
| Line 90: | Line 56: | ||
Look at this table to help explain this notion: | Look at this table to help explain this notion: | ||
| − | <br> | + | [[Image:N_groups.jpg]] |
| + | |||
| + | All content of Lie Algebras and Number of groups from this page can be found from [http://people.maths.ox.ac.uk/craven/docs/lectures/pgroups.pdf here] as well as additional information on these topics. | ||
| + | |||
| + | == <br> The Frattini Subgroup == | ||
| + | |||
| + | '''Definition:''' | ||
== Regular p-groups == | == Regular p-groups == | ||
| Line 132: | Line 104: | ||
For students looking for extensive history on p-groups, Sylow's Theorems and finite simple groups in general you can find this information [http://www.ams.org/journals/bull/2001-38-03/S0273-0979-01-00909-0/S0273-0979-01-00909-0.pdf here] | For students looking for extensive history on p-groups, Sylow's Theorems and finite simple groups in general you can find this information [http://www.ams.org/journals/bull/2001-38-03/S0273-0979-01-00909-0/S0273-0979-01-00909-0.pdf here] | ||
| + | |||
| + | |||
| + | |||
| + | == References == | ||
| + | |||
| + | I've been using these websites: <br>http://math.berkeley.edu/~sikimeti/SylowNotes.pdf<br>http://omega.albany.edu:8008/Symbols.html (this is Tex symbols)<br>http://www.ams.org/journals/bull/2001-38-03/S0273-0979-01-00909-0/S0273-0979-01-00909-0.pdf<br>and also the pdf emailed to you<br>http://groupprops.subwiki.org/wiki/Regular_p-group regular p-group<br>http://people.maths.ox.ac.uk/craven/docs/lectures/pgroups.pdf this one is almost about everything. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
[[Category:MA453Fall2013Walther]] | [[Category:MA453Fall2013Walther]] | ||
Revision as of 12:16, 30 November 2013
Mark Rosinski, markrosi@purdue.edu Joseph Lam, lam5@purdue.edu Beichen Xiao, xiaob@purdue.edu
Outline:
Contents
Email the group to see if anyone else is currently making changes before you begin making changes yourself!!!
P-groups
Definitions:
- Let p be a prime p be an integer greater or equal to 0. A p-group is a group of order pn.
- A subgroup of order pk for some k ≥ 1 is called a p-subgroup.
- If |G| = pαm where p does not divide m, then a subgroup of order pα is called a Sylow p-subgroup of G.
Propositions:
If G is a p-group then G contains an element of order p.
- If G is a p-group then Z(G)cannot be equal to {1}
- Let p be a prime and let G be a group of order p2. Then G is abelian.
- If G is a p-group of order pa, then there exists a chain, {1} is contained in N1 contained in N2 contained in...contained in Na-1 contained in Gof normal subgroups of G, such that |Ni|=pi.
All content above and proofs of these Propositions can be found here
Further Information on p-groups:
- Lie Algebras
- A lie ring is a set R with two binary operations - addition and the Lie bracket - such that
- (R,+) is an abelian group;
- Bilinearity: The bracket operation distributes over addition;
- Alternating on the vector space g: [x,x] = 0 for all x in R;
- The Jacobi Identity: [[x,y],z]+[[y,z],x]+[[z,x],y]=0 for all x,y,z in R.
- If F is a field, and R is an F-vector space with a[x,y]=[ax,y] then R is a Lie algebra.
- To every finite p-group one can associate a Lie ring L(G), and if G/G' is abelian then L(G) is actually a lie algebra over the finite field GF(p).
- Proposition: Let φ be an automorphism of the finite p-group G. Then φ induces an automorphism on L(G), and if φ has order prime to p, then the induced automorphism has the same order.
- A lie ring is a set R with two binary operations - addition and the Lie bracket - such that
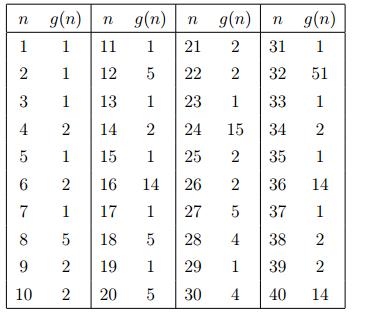
- Number of Groups
- Let g(n) denote the number of groups of order n.
- i) g(p)=1 for p a prime.
- ii) if p<q, then g(pq)=1 if q is not congruent to 1 mod p, and g(pq)=2 otherwise.
- iii) g(p2)=2.
- iv) g(p3)=5.
- Let g(n) denote the number of groups of order n.
From this we can see that the number of groups of order n depends more on the prime structure then on its size.
Look at this table to help explain this notion:
All content of Lie Algebras and Number of groups from this page can be found from here as well as additional information on these topics.
The Frattini Subgroup
Definition:
Regular p-groups
Definitons:
- For every $ a, b \in G $ there exists $ c \in [<a,b>,<a,b>] $ such that apbp = (a'b)pcp
- For every $ a, b \in G $ there exist $ c_1 , c_2 , . . . , c_k \in [<a,b>,<a,b>] $ such that $ a^p b^p = (ab)^p c^p _1 c^p _2 . . . c^p _k $
- For evert $ a, b \in G $ and every natural number n there exist Failed to parse (syntax error): c_1 , c_2 , . . . , c_k \in {,a,b>,<a,b>]
such that $ a^q b^q = (ab)^q c^q _1 c^q _2 . . . c^q _k $ where q = pn
Sylow's Theorems
Notation:
Sylp(G) = the set of Sylow p-subgroups of G
np(G)= the # of Sylow p-subgroups of G =|Sylp(G)|
Theorems:
Let G be a group of order pαm, where p is a prime, m≥1, and p does not divide m. Then:
- Sylp(G) cannot be the empty set.
- All Sylow p-subgroups are conjugate in G. To expand, if P1 and P2 are both Sylow p-subgroups, then there is some g in G such that P1=gP1g-1. In particular, np(G)=(G:NG(P)).
- Any p-subgroup of G is contained in a Sylow p-subgroup
- np(G) is congruent to 1 mod p.
All content from this section and proofs of these Theorems can be found here
Extra Information
For students looking for extensive history on p-groups, Sylow's Theorems and finite simple groups in general you can find this information here
References
I've been using these websites:
http://math.berkeley.edu/~sikimeti/SylowNotes.pdf
http://omega.albany.edu:8008/Symbols.html (this is Tex symbols)
http://www.ams.org/journals/bull/2001-38-03/S0273-0979-01-00909-0/S0273-0979-01-00909-0.pdf
and also the pdf emailed to you
http://groupprops.subwiki.org/wiki/Regular_p-group regular p-group
http://people.maths.ox.ac.uk/craven/docs/lectures/pgroups.pdf this one is almost about everything.