| Line 23: | Line 23: | ||
'''A Look at Weighted Voting''' | '''A Look at Weighted Voting''' | ||
| − | A weighted voting system is one in which the players of such a system hold varying amounts of votes. This differing amount of votes for each player is considered the voting weight of the player. It is completely likely that different players will hold differing weights. We say the voter i has a weight of w<sub>i</sub>. These weights are important when trying to decide the winner of an election. The quota q is the minimum amounts to win said election, and since the voting system is weighted, only certain combinations of wi will decide a winner. This quota should be at least a majority of the sum of | + | A weighted voting system is one in which the players of such a system hold varying amounts of votes. This differing amount of votes for each player is considered the voting weight of the player. It is completely likely that different players will hold differing weights. We say the voter i has a weight of w<sub>i</sub>. These weights are important when trying to decide the winner of an election. The quota q is the minimum amounts to win said election, and since the voting system is weighted, only certain combinations of wi will decide a winner. This quota should be at least a majority of the sum of w<sub>i</sub> to prevent ties, and it is less or equal to the sum of the weights. |
An example of weighted voting used today comes from the World Bank. The World Bank uses weighted voting with its members and board according to the amount of shares the member holds. Each member receives one vote per share of capital stock he or she holds. Therefore, those with higher share holdings will own a higher weight when voting. In fact, this is the most common use of weighted voting today. People involved with shareholder meetings, such as a businesses board of directors, need a voting system that reflects a player’s involvement in that organization. Those with higher shares and investments in a company tend to want to have more weight assigned to their votes in board meetings. Although this is the most common example of weighted voting, this system has emerged in the world of politics as well, especially in the United States. | An example of weighted voting used today comes from the World Bank. The World Bank uses weighted voting with its members and board according to the amount of shares the member holds. Each member receives one vote per share of capital stock he or she holds. Therefore, those with higher share holdings will own a higher weight when voting. In fact, this is the most common use of weighted voting today. People involved with shareholder meetings, such as a businesses board of directors, need a voting system that reflects a player’s involvement in that organization. Those with higher shares and investments in a company tend to want to have more weight assigned to their votes in board meetings. Although this is the most common example of weighted voting, this system has emerged in the world of politics as well, especially in the United States. | ||
| Line 43: | Line 43: | ||
<br>'''The Banzhaf Index of Power (Shuaijia Dai)''' | <br>'''The Banzhaf Index of Power (Shuaijia Dai)''' | ||
| − | A key point we need to keep in mind when we are exploring the weighted voting system is that the weight of a player does not necessarily imply a player's power. For example, it is possible for a weighted voting system with all | + | A key point we need to keep in mind when we are exploring the weighted voting system is that the weight of a player does not necessarily imply a player's power. For example, it is possible for a weighted voting system with all varying number of weights to come down to a one-person, one-vote situation in which case all players have the same power. The power of a player in a weighted voting system can be roughly defined as the ability of the player to influence the final outcome. There are many ways to measure mathematically the power of a player in a weighted voting system. We will introduce a fairly common approach: the Banzhaf power index. |
| − | In order to understand this, | + | In order to understand this concept, let's first give out some definitions in a weighted voting system :<br> |
| + | |||
| + | #<u>'''Coalition'''</u>: A coalition is a collection of voters who agree to vote the same way on a measure. The number of members in this collection can range from no voters to all voters in the system. Since an empty set will make no practical sense, so we usually do not count it. Therefore, the total possible coalitions for a weighted voting system of N voters = 2<sup>N</sup>-1. Also note that coalition is somewhat similar to the concept of sets in mathematics, so we can denote a coalition with the grouping symbol { }. For instance, if there are two voters in the system: P<sub>1</sub>,P<sub>2</sub>. There are 3 possible coalitions in total: {P<sub>1</sub>} , {P<sub>2</sub>}, {P<sub>1</sub>, P<sub>2</sub>}.<sub></sub> | ||
| + | #<u>'''Winning Coalition'''</u>: A coalition that can force the motion to pass. In the above example, if P<sub>1</sub> has 5 votes, P<sub>2</sub> has 3 otes, and the quota q of the system equals 6 (can be represented by {6: 5, 3}. Then the only possible winning coalition is {P<sub>1</sub>, P<sub>2</sub>}. | ||
| + | #<u>'''Critical Player'''</u>: | ||
<br> | <br> | ||
Revision as of 17:03, 27 November 2013
The constitutional right of equal vote vs weighted voting: historical events and the Banzhaf power index
A team project for MA279, Fall 2013
Team members: Shuaijia Dai, Bo Ling, Rustam Orazaliyev, Matthew D Parr, Christopher Patrick
Don't copy and paste, the page goes mad. Make sure to paraphrase everything you write and include references for it.
I. Introduction. (Bo Ling)
(SECTION 2. The right of citizens of the United States to vote and to participate in elections on an equal basis shall not be denied or abridged by the United States or any State on account of political-party affiliation or prior condition of incarceration.)
II. Equal vote definition, example, where it is used. Equal voting Historical Timeline in the USA. (Christopher Patrick)
III. Weighted voting definition, example, where it is used. When the US started to use it
A Look at Weighted Voting
A weighted voting system is one in which the players of such a system hold varying amounts of votes. This differing amount of votes for each player is considered the voting weight of the player. It is completely likely that different players will hold differing weights. We say the voter i has a weight of wi. These weights are important when trying to decide the winner of an election. The quota q is the minimum amounts to win said election, and since the voting system is weighted, only certain combinations of wi will decide a winner. This quota should be at least a majority of the sum of wi to prevent ties, and it is less or equal to the sum of the weights.
An example of weighted voting used today comes from the World Bank. The World Bank uses weighted voting with its members and board according to the amount of shares the member holds. Each member receives one vote per share of capital stock he or she holds. Therefore, those with higher share holdings will own a higher weight when voting. In fact, this is the most common use of weighted voting today. People involved with shareholder meetings, such as a businesses board of directors, need a voting system that reflects a player’s involvement in that organization. Those with higher shares and investments in a company tend to want to have more weight assigned to their votes in board meetings. Although this is the most common example of weighted voting, this system has emerged in the world of politics as well, especially in the United States.
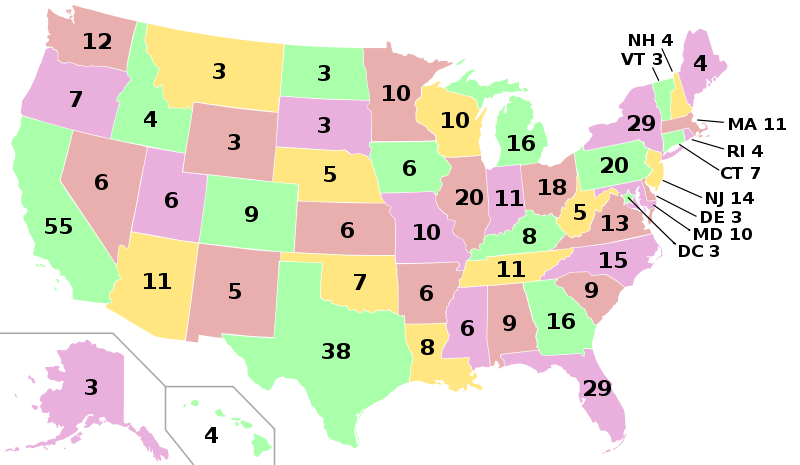
Today, the United States of America uses a weighted voting system in what most consider its most important election–the presidential election. Weighted voting entered mainstream American politics with the creation of the Electoral College in 1787. In the Electoral College system, each state is allotted a certain number of electors representative of the state’s congressional delegation. Essentially, the Electoral College acts as a weighted voting system to elect the President. There are 56 players: 50 states, the District of Columbia, three Nebraska congressional districts, and two Maine congressional districts. The number of electors assigned to each player acts as the player’s weight, and these weights vary as each state could have a different congressional delegation. The weights range from 1 (for individual congressional districts) to 55 (for California’s delegation), and the quota of 270 is the simple majority of the sum of the weights, 538.
Clearly, the weighted voting system is implemented all over the world in differing organizations and governments. However, this system brings with it more interesting things to consider. Since the weights of players can be all different, a critical question arises. Who controls elections? This leads to the study of what a player’s power is in such a voting system. One of the most common ways to determine power is through the Banzhaf Power Index. A study of this index is essential to understanding weighted voting systems.
References:
The Banzhaf Index of Power (Shuaijia Dai)
A key point we need to keep in mind when we are exploring the weighted voting system is that the weight of a player does not necessarily imply a player's power. For example, it is possible for a weighted voting system with all varying number of weights to come down to a one-person, one-vote situation in which case all players have the same power. The power of a player in a weighted voting system can be roughly defined as the ability of the player to influence the final outcome. There are many ways to measure mathematically the power of a player in a weighted voting system. We will introduce a fairly common approach: the Banzhaf power index.
In order to understand this concept, let's first give out some definitions in a weighted voting system :
- Coalition: A coalition is a collection of voters who agree to vote the same way on a measure. The number of members in this collection can range from no voters to all voters in the system. Since an empty set will make no practical sense, so we usually do not count it. Therefore, the total possible coalitions for a weighted voting system of N voters = 2N-1. Also note that coalition is somewhat similar to the concept of sets in mathematics, so we can denote a coalition with the grouping symbol { }. For instance, if there are two voters in the system: P1,P2. There are 3 possible coalitions in total: {P1} , {P2}, {P1, P2}.
- Winning Coalition: A coalition that can force the motion to pass. In the above example, if P1 has 5 votes, P2 has 3 otes, and the quota q of the system equals 6 (can be represented by {6: 5, 3}. Then the only possible winning coalition is {P1, P2}.
- Critical Player:
, and Banzhaf index relation to our historical events. (Shuaijia Dai)
V. Problems with weighted voting and historical events.
Nowadays, social inequality is considered to be one of the biggest problems the modern society faces. Therefore, the majority of developed countries, especially the US launch programs and invest big amounts of money to fight with social inequality. However, what the US government forgets about is its own voting system. The United States of America uses weighted voting system in the presidential election. Considering the fact how important the principle of equality nowadays is, the use of weighted voting system in such a developed country is at least unexpected.
As it can be seen on the following image (Electoral college, 2012), states and District of Columbia represent players, while their electors act like weights.
The District of Columbia and all states, except Nebraska and Maine follow winner-takes-all rule. According to the rule, candidate with the most votes gets all of the state's votes. Obviously winner-takes-all rule ignores the opinion of those who did not vote for the winning candidate, since their votes will not be considered afterwards. As a result, it can lead to the election in which the candidate with the most popular votes does not win the election, and it has already happened several times.
| Year | Most popular votes candidate |
Winner of the election | Votes for the most popular candidate | Votes for the election winner | Difference |
| 1824 | Andrew Jackson | John Q. Adams | 151 271 | 113 122 | 38 149 |
| 1876 | Samuel J. Tilden | Rutherford B. Hayes | 4 288 191 | 4 033 497 | 254 694 |
| 1888 | Grover Cleveland | Benjamin Harrison | 5 539 118 | 5 449 825 | 89 293 |
| 2000 | Al Gore | George W. Bush | 50 992 335 | 50 445 156 | 537 179 |
Obviously such elections ignore the majority opinion and violate the principle of equality, when all voters are equal. In other words, outcomes of these elections does not follow the basic principles of democracy.
As it was mentioned before, to win the election, a candidate must recieve at least 270 of electoral votes. As a result, it is possible to win the election by winning in eleven states having the largest weights. California, Texas, New York, Florida, Pennsylvania, Illinois, Ohio, Georgia, Michigan, North Carolina, and New Jersey give 270 votes. According to population estimate, July1, 2012, these states have a population combined about 178,591,446, or 57.07% of total population of the United States. However, since all of these states follow winner-takes-all rule, recieving 50.1% of votes in every of these states would also result in winning the election. In other words, even though it is highly unlikely but theoretically it is possible to win the presidential election by receving only 28.60% (57.07*0.501) of votes, assuming that amount of voters is proportional to the state's population.
VI. Conclusion. (Bo Ling)
Reference.
[4] U. S. Electoral College: FAQ
[5] List of U.S. States and territories by population