| Line 71: | Line 71: | ||
'''Crystal Movement and Symmetry'''<br><hr><br> | '''Crystal Movement and Symmetry'''<br><hr><br> | ||
'''Combinations of Symmetry Operations'''<br><hr><br> | '''Combinations of Symmetry Operations'''<br><hr><br> | ||
| − | There are | + | Symmetry within a crystal is a systematic repetition of the structural features of the crystal. <br> |
| − | + | There are two main types of symmetry that exist within a crystal system. The first of the symmetries <br> | |
| + | is translational symmetry, which is the symmetry across a length or an area/volume. The other type of <br> | ||
| + | symmetry is point symmetry, which is the repetition of something around a point. There are four different <br> | ||
| + | types of point symmetry operations, reflection, rotation, inversion, and rotoinversion. Reflection is when <br> | ||
| + | one side of the crystal matches the other side of the crystal across a plane. A rotation occurs when the <br> | ||
| + | crystal is rotated a certain amount of degrees before it repeats itself. An inversion occurs when a line <br> | ||
| + | is drawn through the center and matches up with another feature of the crystal. A rotoinversion is when <br> | ||
| + | a rotation is performed with an inversion. <br><br> | ||
| + | When looking at all the different symmetry operations that a crystal structure can possess, crystals can <br> | ||
| + | be grouped into several different crystal systems. | ||
'''Crystal Symmetry Groups'''<br><hr><br> | '''Crystal Symmetry Groups'''<br><hr><br> | ||
'''References and Links'''<br><hr> | '''References and Links'''<br><hr> | ||
Revision as of 12:31, 27 November 2013
Crystals and Symmetry
NamesJason Krupp (krupp@purdue.edu)
Erik Plesha (eplesha@purdue.edu)
Andrew Wightman (awightma@purdue.edu)
Thilagan Sekaran(trajasek@purdue.edu)
A) Crystal Symmetries Introduction
- Miller Indices
- Crystal Structures
- Slip Systems
B) Crystal Movement and Symmetry
- Translational Movement
- Rotational Movement
- Mirror Movement
C) Combinations of Symmetry Operations
- 32 Crystal Classes
D) Crystal Symmetry Groups
- Finite Symmetry Groups
- Non-Finite Symmetry Groups
Many important material properties depend on crystal structure. Some of these
include the following inexhaustive list: conductivity, magnetism, stiffness, and
strength.
Miller Indices represent an efficient way to label the orientation of the crystals.
For planes, the Miller Index value is the reciprocal of the value of the
intersection of the plane with a particular axis, converted to whole numbers and are
usually represented by round brackets (parenthesis). For directions in a crystal
lattice, the index is the axis coordinate of the end point of the vector, converted
to the nearest whole number and are usually represented by [square brackets].
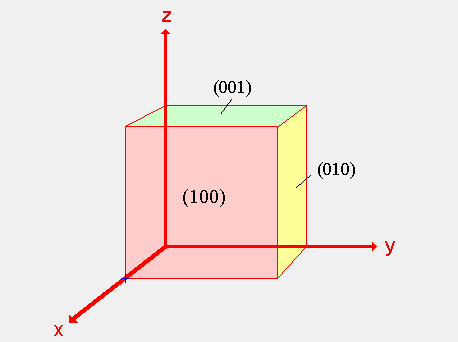
For example, the figure above depicts 3 of the 6 cube faces and the corresponding
Miller Indices. The red plane is labeled as (100) because the plane is shifted 1
unit in the x-direction. The yellow plane is labeled (010) because it is shifted 1
unit in the y-direction. Finally, the green plane is labeled (001) because it is
shifted 1 unit in the z-direction. For more on Miller Indices, please visit the
link listed in the References Section.
Although Miller Indices do a great job of describing crystals, it doesn't complete
the task. Crystals can also be divided up according to their structure, the three most
common types being FCC (Face-Centered Cubic), BCC (Body-Centered Cubic), and SC
(Simple Cubic) structures.
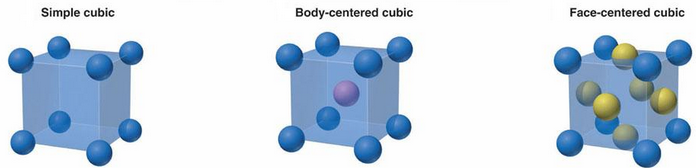
As you can see, the above figure shows the three aforementioned crystal types. The
body-centered cubic structure is similar to the simple cubic structure but with an added
atom in the center of the unit cell. The face-centered cubic structure is also similar
to the simple cubic structure but with added atoms in the center of all 6 cube faces.
These structures can also be defined by their coordination numbers, or the number of
nearest neighboring atoms. For the simple cubic structure, there are 6 nearest neighbors,
corresponding to a coordination number of 6. The face-centered cubic structure has a
coordination number of 12 and the body-centered cubic structure has a coordination number
of 8.
A slip system is a combination of a slip direction and a slip plane. A slip plane is a plane
in which the planar density is largest. For the FCC crystal structure, the slip plane is
labeled (111) because this plane is most densely populated with atoms and has the smallest
amount of free space. The slip direction is the most densely populated direction of a crystal;
this is the [110] direction for FCC crystals. With increasing load to the crystal, the slip
plane and direction align parallel to the tensile stress axis. Under extreme tension, crystal
fracture may be observed.
Combinations of Symmetry Operations
Symmetry within a crystal is a systematic repetition of the structural features of the crystal.
There are two main types of symmetry that exist within a crystal system. The first of the symmetries
is translational symmetry, which is the symmetry across a length or an area/volume. The other type of
symmetry is point symmetry, which is the repetition of something around a point. There are four different
types of point symmetry operations, reflection, rotation, inversion, and rotoinversion. Reflection is when
one side of the crystal matches the other side of the crystal across a plane. A rotation occurs when the
crystal is rotated a certain amount of degrees before it repeats itself. An inversion occurs when a line
is drawn through the center and matches up with another feature of the crystal. A rotoinversion is when
a rotation is performed with an inversion.
When looking at all the different symmetry operations that a crystal structure can possess, crystals can
be grouped into several different crystal systems.
References and Links
Gallian, J. (2013). Contemporary abstract algebra. (8th ed.). Boston, MA: Brooks/Cole, Cengage Learning.
Jacobson, L. A. (2008). Crystal symmetries - physical metallurgy. Unpublished manuscript, METE 327, Retrieved from
http://infohost.nmt.edu/~ljacobso/crystalslides.pdf