| Line 111: | Line 111: | ||
Due to the long computation times and inaccuracies brought about by hardware limitations involved when calculating elliptic curves over real numbers, the curves are often instead calculated over the fields ''F<sub>p</sub>'' or ''F<sub>2m</sub>''. Since the field ''F<sub>p</sub>'' contains only integer elements, there is no rounding error associated with doing calculations along the curves since every result is exact. For Fp, the elliptic curve equation becomes ''y<sup>2</sup> mod p = ''x<sup>3</sup> + ax + b ''mod p. Each set of coefficients a,b and each p (prime) chosen is associated with a set of points that can exist along the curve (assuming no repeated factors in ''x<sup>3</sup> + ax + b ''). This is a major difference from using the field of real numbers, where there were an infinite number of points along the curve. Due to the finite solutions to the equation, the plot of points for a curve group over ''F<sub>p</sub>''does not actually resemble a curve. As such, the geometric methods used for calculating over real numbers cannot be employed. Instead, algebraic rules are used:<br>[[Image:Topic13 5.png]] '' | Due to the long computation times and inaccuracies brought about by hardware limitations involved when calculating elliptic curves over real numbers, the curves are often instead calculated over the fields ''F<sub>p</sub>'' or ''F<sub>2m</sub>''. Since the field ''F<sub>p</sub>'' contains only integer elements, there is no rounding error associated with doing calculations along the curves since every result is exact. For Fp, the elliptic curve equation becomes ''y<sup>2</sup> mod p = ''x<sup>3</sup> + ax + b ''mod p. Each set of coefficients a,b and each p (prime) chosen is associated with a set of points that can exist along the curve (assuming no repeated factors in ''x<sup>3</sup> + ax + b ''). This is a major difference from using the field of real numbers, where there were an infinite number of points along the curve. Due to the finite solutions to the equation, the plot of points for a curve group over ''F<sub>p</sub>''does not actually resemble a curve. As such, the geometric methods used for calculating over real numbers cannot be employed. Instead, algebraic rules are used:<br>[[Image:Topic13 5.png]] '' | ||
| − | <br>For when P = -Q: P + Q = O, as in the case for real numbers. Likewise, 2P = O if | + | <br>For when P = -Q: P + Q = O, as in the case for real numbers. Likewise, 2P = O if ''P<sub>y</sub>'' = 0. |
| − | <br> Cryptosystems rely on difficult mathematical problems that are computationally infeasible to solve. This makes the discrete logarithm problem a widely used basis for cryptographic systems since there is no known general method of efficiently computing them. The discrete logarithm is the inverse operation of modular exponentiation; it tries to find the solution to a | + | <br> Cryptosystems rely on difficult mathematical problems that are computationally infeasible to solve. This makes the discrete logarithm problem a widely used basis for cryptographic systems since there is no known general method of efficiently computing them. The discrete logarithm is the inverse operation of modular exponentiation; it tries to find the solution to ''a<sup>n</sup>''=b where a and b are known elements of a group. For an elliptic curve group defined over ''F<sub>p</sub>'', a problem occurs: Successive additions of P to 2P may be done to yield a result nP, but n may not be able to directly be found if only the starting point P and end point nP are known. The simple approach of iterating through all possibile values of n and calculating nP for each case is computationally expensive, and impractical for large values of n used with large elliptic curve groups. |
| − | <br> From here it can be seen how a cryptosystem would be developed from elliptic curves. Initially, domain parameters are publicly agreed upon by two parties. These parameters are: a,b, the coefficients for the elliptic curve; P, the starting point (which is a generator of the elliptic curve group); and the value of p (prime) for the field | + | <br> From here it can be seen how a cryptosystem would be developed from elliptic curves. Initially, domain parameters are publicly agreed upon by two parties. These parameters are: a,b, the coefficients for the elliptic curve; P, the starting point (which is a generator of the elliptic curve group); and the value of p (prime) for the field ''F<sub>p</sub>'' on which the elliptic curve is defined over. Next, the two parties independently generate a private key, n, and a public key, K = nP. The public keys are made publicly available by each party. As previously mentioned, due to the discrete logarithm problem, the private key n cannot be determined knowing only K and P. Once the public keys are shared, each party may add the other party’s public key n successive times (n being their own private key) to determine a shared result: (''n<sub>1</sub>'' + ''n<sub>2</sub>'')P. Both people will come to the same result, which is the secret information being shared. Anybody listening in on this exchange can not reproduce the same result without knowing one of the n values. Provided that each party keeps their private key a secret and that the domain parameters and private keys were chosen with some intelligence, the n values will be infeasible to solve for. This process is typically used for key agreement and is called elliptic-curve Diffie-Helman. Since the result is shared and only known by the two parties, the result is may be used as a key for use with a symmetric key cipher for the exchange of actual private information once the key has been established. |
<br>Of course, this is not the only way elliptic curves may be used in cryptosystems. For example, with a slight complication to the process above, a system can be devised to share information rather than just be for key generation, as is the case with the process known as the Integrated Encryption Scheme. There are several practical applications of elliptic curves to the problem of sharing private information.<br> | <br>Of course, this is not the only way elliptic curves may be used in cryptosystems. For example, with a slight complication to the process above, a system can be devised to share information rather than just be for key generation, as is the case with the process known as the Integrated Encryption Scheme. There are several practical applications of elliptic curves to the problem of sharing private information.<br> | ||
Revision as of 17:18, 24 November 2013
Contents
[hide]Elliptic curves and public key cryptography
By Dan Klanke, Brandon Myers, Antong Li and Chenghao Cai
Abstract
Along with the rapid development of modern communication network, especially the Internet, using the Internet as an information communication and processing is becoming more and more common. Traditional social affairs and business operation model are facing the unprecedented impact. At present, both governments and enterprises are integrated into the Internet revolution, from its traditional management mode to the network schema evolution. The future of e-government, e-commerce, electronic business will become an irreversible trend. In the growing network activities, people are becoming more and more concerned about the information security problem, which includes: confirming customer's true identity, personal or confidential information system and data protection, preventing illegal data modification, and non-repudiation for the behavior under the network environment.
Thus improving the security level of cryptography, the most core technology in information security, is brought to the table. Based on the difficulty of solving the discrete logarithm problem on a general elliptic curve, Neal Koblitz and Victor S. Miller proposed an elliptic curve cryptosystem. Cryptosystem based on elliptic curves offer the benefits of good realization using hardware and software, smaller bandwidth, smaller memory and etc. These benefits make elliptic curve cryptosystems be a new promising area in public-key cryptography.
In this report, the principal of public key cryptography is discussed, represented by the asymmetric cryptography Diffie-Hellman and RSA systems, which are based on number theory. Then, the properties and application of elliptic curve cryptosystem, together with the operation guides are explained. Finally, the reasons of causing the difference of asymmetric cryptography and elliptic curve cryptography deepen the understanding of the algebraic geometry field.
Intro to Public Key Cryptography
Public key cryptography also known as asymmetric cryptography refers to a cryptographic algorithm which requires two separate keys one of which is secret and one of which is public. Although different, the two parts of this key pair are mathematically linked. The public key is used to encrypt plaintext or to verify a digital signature; whereas the private key is used to decrypt ciphertext or to create a digital signature. The term "asymmetric" stems from the use of different keys to perform these opposite functions, each the inverse of the other.
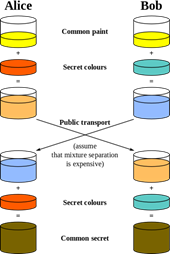
Cryptography is a way for two people, commonly referred to as Alice (A) and Bob (B), to communicate over an insecure communications channel without an opponent, Eve (E), intercepting what is being said. It provides the foundation for key management and digital signatures, both integral parts of any cryptosystem. Below is a pictorial representation illustrating the general idea of key exchange.
Usage / Current Applications
Key Management:
Key Management entails the generation, exchange, storage, use, and replacement of keys. It includes cryptographic protocol design, key servers, user procedures, and other relevant protocols. Successful key management is critical to the security of a cryptosystem.
Digital Signatures:
A digital signature is a mathematical scheme for demonstrating the authenticity of a digital message or document. A valid digital signature gives a recipient reason to believe that the message was created by a known sender, such that the sender cannot deny having sent the message and that the message was not altered in transit.
Principle of Operation
Public and private keys:
Alice and Bob each have a key, some number or mathematical procedure that can be applied to messages, composed of a public piece and a private piece. The private pieces of these keys are never transmitted, while the public pieces are accessible to everyone.
Based on mathematics:
Public-key algorithms are based on mathematical problems which currently admit no efficient solution that are inherent in certain integer factorization, discrete logarithm, and elliptic curve relationships.
Authentication:
Alice and Bob may also have public and private signatures, which work similarly to the keys. If Alice wants Bob to know that the message he receives from her is authentic, she’ll apply a private signature to some authentication message before sending it; when Bob wants to know that it’s hers, he’ll apply the easily accessible public part of her signature to that, which will return the authentication.
Asymmetric Cryptography Systems
First Generation:
Internet communications have been secured by the first generation of public key cryptographic algorithms developed in the mid-1970's. Notably, they form the basis for key management and authentication for IP encryption (IKE/IPSEC), web traffic (SSL/TLS) and secure electronic mail. Examples of such are the Diffie – Hellman and RSA methods.
Diffie-Hellman:
Diffie–Hellman key exchange (D–H) is a specific method of exchanging cryptographic keys. It is a first generation of key exchange implemented within the field of cryptography. The Diffie–Hellman key exchange method allows two parties that have no prior knowledge of each other to jointly establish a shared secret key over an insecure communications channel. This key can then be used to encrypt subsequent communications using a symmetric key cipher, so that a third party cannot intercept the message. The Diffie-Hellman method makes use of certain one-way functions called trap-door functions, to make it almost impossible to decipher encrypted data without a key.
RSA:
Known as one of the first practicable public-key cryptosystems and is yet widely used for secure data transmission. In RSA, this asymmetry is based on the practical difficulty of factoring the product of two large prime numbers, the factoring problem. RSA stands for Ron Rivest, Adi Shamir and Leonard Adleman, who first publicly described the algorithm in 1977.
Intro to elliptic curves in public key cryptography
In 1985, two American mathematician Neal Koblitz and Victor S. Miller suggested the use of elliptic curves in cryptography for the first time independently. Before this, another algorithm called Rivest-Shamir-Adleman (RSA) is already published in 1970s. RSA is the very first well-established public key cryptosystem and it is wildly used after publishing. Elliptic Curve Cryptography (ECC) often used to compare with RSA after Koblitz and Miller suggested it. According to an IEEE article Performance Analysis of Identity Management in the Session Initiation Protocol by Rebahi, Pallares, Nguyen and etc, ECC encryption only need 160-bit keys to provide equivalent level of security while RSA encryption needs 1024 bits. More details for the key size is shown in the following table:
| ECC key size(bits) | RSA key size(bits) | Key size ratio |
| 160 | 1024 | 1:6 |
| 224 | 2048 | 1:9 |
| 256 | 3072 | 1:12 |
| 384 | 7680 | 1:20 |
| 512 | 15360 | 1:30 |
Even though ECC is efficient, it has a few drawbacks just like other algorithms. ECC requires more complicated operation than RSA, so it is harder to verify whether a specific implementation is correct or not. Therefore ECC has higher possibility of operation errors. However, ECC is still one of the most efficient and popular cryptography so far.Also, in another paper The Advantages of Elliptic Curve Cryptography For Wireless Security written by K. Lauter in February 2004, she wrote “Wireless devices are rapidly becoming more dependent on security features such as the ability to do secure email, secure Web browsing, and virtual private networking to corporate networks, and ECC allows more efficient implementation of all of these features.” So ECC is particularly crucial in small cards or portable devices where CPU consumption, battery life and memory usage are limited. In this high-technology era, ECC is extremely wild used.
The Mathematics of Elliptic Curves
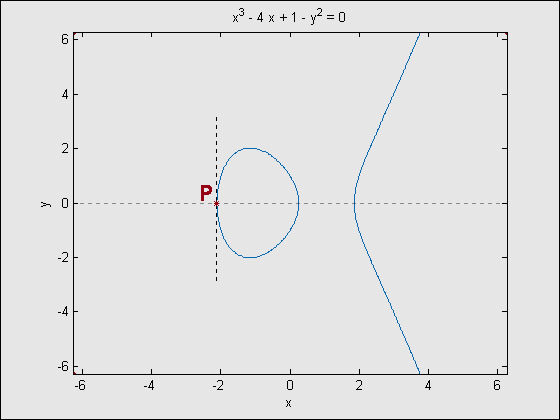
An elliptic curve over a group is the set of points which satisfy an elliptic curve equation, which takes the form:y2 = x3 + x + b where a and b are coefficients belonging to the group the elliptic curve is defined over. Varying a and b will give different elliptic curves. These curves are symmetric on the x-axis, and, barring a few exceptions, a tangent taken at any point or any line drawn between two curve points will intersect the curve at exactly one other point. These three properties are important for forming an algebraic group from these curves.
Cryptosystems often take advantage of the properties of algebraic groups to function. Provided that x3 + ax + b contains no repeated factors, the elliptic curve may be used to form such a group. This group contains elements from the field the curve was defined over, as well as a point O at infinity which serves as the additive identity.
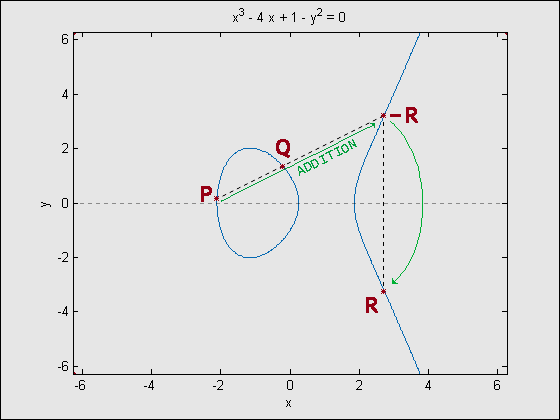
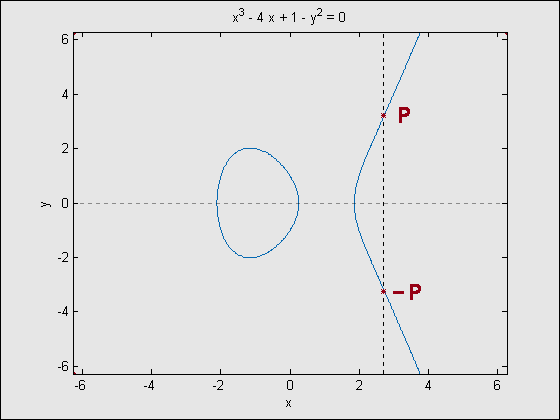
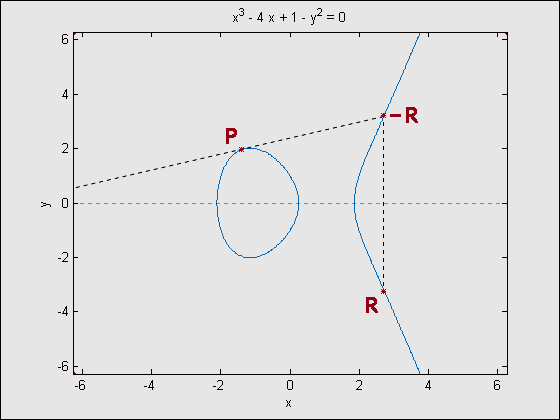
Addition in elliptic curve groups can be described geometrically, and is more easily understood visually. All examples given here are for an elliptic curve over real numbers. Negation of a point P = (x,y) results in the reflection of the point across the x-axis. Since the curve is symmetric on the x-axis, the point –P = (x,-y) will always be on the curve. Addition of two unique points, P and Q, is done by finding the point at which the line through P and Q intersects the curve again, then taking the negative of the intersection point. As mentioned above, this will only ever be at one point due to the properties of elliptic curves. A special case occurs for addition of P and –P. Since the the line through P and –P is a vertical, it will never intersect the elliptic curve other than at P and –P. As such, this is why the point at infinity, O, is included in the group’s elements, allowing the addition of P and –P be: P+(-P)= O. Addition of a point with itself is done by finding the intersection of the line tangent to the point and the elliptic curve, then negating that intersection point. However, for points with a zero y-coordinate, the tangent line will not intersect the curve at any other point. In this case, the double of the point is O.
Figure 1- Addition of two points: P + Q = R
Figure 2 – Addition of a point with its negative: P + (-P) = O
Figure 3 – Addition of a point with itself: 2P = R
Figure 4 – Addition with a point with itself when P = (x,0): 2P = 0
Due to the long computation times and inaccuracies brought about by hardware limitations involved when calculating elliptic curves over real numbers, the curves are often instead calculated over the fields Fp or F2m. Since the field Fp contains only integer elements, there is no rounding error associated with doing calculations along the curves since every result is exact. For Fp, the elliptic curve equation becomes y2 mod p = x3 + ax + b mod p. Each set of coefficients a,b and each p (prime) chosen is associated with a set of points that can exist along the curve (assuming no repeated factors in x3 + ax + b ). This is a major difference from using the field of real numbers, where there were an infinite number of points along the curve. Due to the finite solutions to the equation, the plot of points for a curve group over Fpdoes not actually resemble a curve. As such, the geometric methods used for calculating over real numbers cannot be employed. Instead, algebraic rules are used: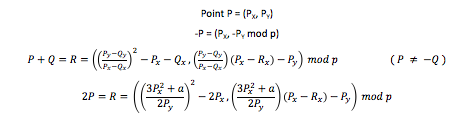
For when P = -Q: P + Q = O, as in the case for real numbers. Likewise, 2P = O if Py = 0.
Cryptosystems rely on difficult mathematical problems that are computationally infeasible to solve. This makes the discrete logarithm problem a widely used basis for cryptographic systems since there is no known general method of efficiently computing them. The discrete logarithm is the inverse operation of modular exponentiation; it tries to find the solution to an=b where a and b are known elements of a group. For an elliptic curve group defined over Fp, a problem occurs: Successive additions of P to 2P may be done to yield a result nP, but n may not be able to directly be found if only the starting point P and end point nP are known. The simple approach of iterating through all possibile values of n and calculating nP for each case is computationally expensive, and impractical for large values of n used with large elliptic curve groups.
From here it can be seen how a cryptosystem would be developed from elliptic curves. Initially, domain parameters are publicly agreed upon by two parties. These parameters are: a,b, the coefficients for the elliptic curve; P, the starting point (which is a generator of the elliptic curve group); and the value of p (prime) for the field Fp on which the elliptic curve is defined over. Next, the two parties independently generate a private key, n, and a public key, K = nP. The public keys are made publicly available by each party. As previously mentioned, due to the discrete logarithm problem, the private key n cannot be determined knowing only K and P. Once the public keys are shared, each party may add the other party’s public key n successive times (n being their own private key) to determine a shared result: (n1 + n2)P. Both people will come to the same result, which is the secret information being shared. Anybody listening in on this exchange can not reproduce the same result without knowing one of the n values. Provided that each party keeps their private key a secret and that the domain parameters and private keys were chosen with some intelligence, the n values will be infeasible to solve for. This process is typically used for key agreement and is called elliptic-curve Diffie-Helman. Since the result is shared and only known by the two parties, the result is may be used as a key for use with a symmetric key cipher for the exchange of actual private information once the key has been established.
Of course, this is not the only way elliptic curves may be used in cryptosystems. For example, with a slight complication to the process above, a system can be devised to share information rather than just be for key generation, as is the case with the process known as the Integrated Encryption Scheme. There are several practical applications of elliptic curves to the problem of sharing private information.
The standards of elliptic curve cryptography
With all the advantages, ECC will replace the RSA in some areas, such as PDA, mobile phones, smart card application, and become the general public key encryption algorithm. Many international organizations for standardization (government, industry, finance, business, etc.) have all kinds of elliptic curve cryptosystem, as their standardization documents issued all over the world.
ECC standards can be divided into two forms: one kind is technical standard, described as the ECC system mainly supported by technology, including IEEEP1363, ANSI X9.62, ANSI X9.63, SEC1, SEC2, FIP 186-2, ISO/IEC 14888-3. This standard normalizes the selection of various ECC parameters, and gives a group of ECC parameters under different strength levels of safety. Another kind of standard is the applicable standard, which is the recommendation for the usage under specific application environment ECC technology, mainly has the ISO/IEC 15946, IETF PKIX, IETF TLS, WAP WTLS, etc.
At the same time of standardizing the elliptic curve cryptography, some encryption, signature and key exchange software and hardware based on the standard elliptic curve have also appeared. RSA Security LLC, a United States company, released BSAFE 4.0, containing an ECC password engine toolkit in 1997. With the help of the industry, leading by a security company in Canada called Certicom, also developed and produced the password products based on elliptic curve cryptography and raised rewarded challenges on security attacks on elliptic curve cryptography under various conditions. With all these companies putting the efforts on research and practices, ECC technology will surely be more and more widely used in the field of information security.
Conclusion
With the development and application of information technology, the problem of information security becomes more and more important. In order to improve the security, secrecy and reliability of communication, we need cryptosystem of high dependability and good security. The elliptic curve cryptosystem provides the highest strength of any cryptosystem known. Because its shorter key size, less computation, less memory space and lower bandwidth, the application prospect in information field of the elliptic curve cryptosystem will keep growing as it become more sophisticated though years of research and practice.
Reference:
Hendrix, Joe. April 8, 2013. Elliptic Curve Cryptography.
http://www.linuxjournal.com/content/elliptic-curve-cryptography
Leslie, Martin. Class Handout.
http://math.arizona.edu/~mleslie/files/handout.pdf
January 15, 2009. The Case for Elliptic Curve Cryptography.
http://www.nsa.gov/business/programs/elliptic_curve.shtml
Class Handout. Elliptic Curves in Public Key Cryptography: The Diffie Hellman Key Exchange Protocol and its Relationship to the Elliptic Curve Discrete Logarithm Problem.
http://ocw.mit.edu/courses/mathematics/18-704-seminar-in-algebra-and-number-theory-rational-points-on-elliptic-curves-fall-2004/projects/haraksingh.pdf
Brow, Elaine. December 2010. Elliptic Curve Cryptography.
http://www.math.hmc.edu/~ursula/teaching/math189/finalpapers/elaine.pdf
Rebahi. Y, Pallares. J. J, Nguyen. T.M, and etc, 2008, Performance Analysis of Identity Management in the Session Initiation Protocol
http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=4493606&isnumber=4493499&tag=1
K. Lauter, February 2004, The Advantages of Elliptic Curve Cryptography For Wireless Security
http://research.microsoft.com/en-us/um/people/klauter/IEEEfinal.pdf