| Line 111: | Line 111: | ||
It is easy to extrapolate, then, that the transformation from one set of coordinates to another set is merely | It is easy to extrapolate, then, that the transformation from one set of coordinates to another set is merely | ||
| − | <font size=4><math> | + | <font size=4><math> dC2=det(J(T))dC1 </math></font> |
where C1 is the first set of coordinates, det(J(C1)) is the determinant of the Jacobian matrix made from the Transformation T, T is the Transformation from C1 to C2 and C2 is the second set of coordinates. | where C1 is the first set of coordinates, det(J(C1)) is the determinant of the Jacobian matrix made from the Transformation T, T is the Transformation from C1 to C2 and C2 is the second set of coordinates. | ||
| Line 124: | Line 124: | ||
<math>T(u)=\begin{matrix}u^2\end{matrix}=\begin{matrix}x\end{matrix}</math> | <math>T(u)=\begin{matrix}u^2\end{matrix}=\begin{matrix}x\end{matrix}</math> | ||
| − | <math>~~~,~~~~~~~~ J(u)=\begin{bmatrix}\frac{\partial x}{\partial u}\end{bmatrix}=\begin{bmatrix}2u\end{bmatrix} </math><math>,~~~~~~~ | + | <math>~~~,~~~~~~~~ J(u)=\begin{bmatrix}\frac{\partial x}{\partial u}\end{bmatrix}=\begin{bmatrix}2u\end{bmatrix} </math><math>,~~~~~~~ du=\left|J(u)\right|\times du=2u\times dx </math> |
| + | Remember that when substituting, to be VERY careful. If you substitute from the <x,y>= direction, then the previous formula was correct. However, if you you substitute from the <u,v>= direction, then you need to have the Jacobian on the other side. What do I mean? | ||
| + | it should always be the case where | ||
| + | |||
| + | <math> J(\vec u) \times d\vec x = d\vec u, J(\vec x) \times d\vec u = d\vec x </math>. | ||
| + | |||
| + | Let's do some examples to show what I mean. | ||
====Example #4:==== | ====Example #4:==== | ||
| Line 146: | Line 152: | ||
<math> \int^{16}_9 \int^{14}_6 k(u,v)\mathrm{d}u\mathrm{d}v</math> | <math> \int^{16}_9 \int^{14}_6 k(u,v)\mathrm{d}u\mathrm{d}v</math> | ||
| + | |||
| + | However, notice that in this case, instead of substituting <x,y>=, we're substituting from <u,v>= perspective. This means that we will have to divide the determinant of the Jacobian from the <u,v> side instead of multiplying it. | ||
<font size = 4> | <font size = 4> | ||
| Line 162: | Line 170: | ||
</math> | </math> | ||
| − | <math> | + | <math> dudv= \left|J(u,v)\right|\times dxdy |
| − | + | \longrightarrow \left|\begin{matrix} | |
2y & 2x \\ | 2y & 2x \\ | ||
| − | 2x & -2y\end{matrix}\right|\times dudv=(4y^2+4x^2) | + | 2x & -2y\end{matrix}\right|\times dudv=(4y^2+4x^2)dxdy </math> |
The new region looks like this: [[Image: JacobianPic4.png|200px]] | The new region looks like this: [[Image: JacobianPic4.png|200px]] | ||
| Line 186: | Line 194: | ||
There are many ways to approach this, but to start, let's choose the change of variables to be | There are many ways to approach this, but to start, let's choose the change of variables to be | ||
| − | + | x=u/2, y=v/3. Why? | |
<math> (2x)^2+(3y)^2=36\longrightarrow u^2+v^2=36 </math> | <math> (2x)^2+(3y)^2=36\longrightarrow u^2+v^2=36 </math> | ||
| Line 193: | Line 201: | ||
We've turned the region from an ellipse to a circle! | We've turned the region from an ellipse to a circle! | ||
| + | |||
| + | Notice that in this case, we're substituting from the <x,y> side, meaning that the jacobian will be flipped. | ||
<font size = 4> | <font size = 4> | ||
| − | <math> | + | <math>x=u/2\longrightarrow \frac{\partial x}{\partial u}= 1/2 , \; \frac{\partial x}{\partial v} = 0</math> |
| − | <math> | + | <math>y=v/3\longrightarrow \frac{\partial y}{\partial u}=0 , \; \frac{\partial y}{\partial v} =1/3</math> |
</font> | </font> | ||
| − | <math>J( | + | <math>J(x,y)=\begin{bmatrix} |
| − | \frac{\partial | + | \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ |
| − | \frac{\partial | + | \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \end{bmatrix}= |
\begin{bmatrix} | \begin{bmatrix} | ||
| − | 2 & 0 \\ | + | 1/2 & 0 \\ |
| − | 0 & 3\end{bmatrix} | + | 0 & 1/3\end{bmatrix} |
</math> | </math> | ||
| − | <math> dxdy=\left|J( | + | <math> dxdy=\left|J(x,y)\right| \times dudv |
=\left|\begin{matrix} | =\left|\begin{matrix} | ||
| − | 2 & 0 \\ | + | 1/2 & 0 \\ |
| − | 0 & 3\end{matrix}\right|\times dudv=(6)dudv </math> | + | 0 & 1/3\end{matrix}\right|\times dudv=(1/6)dudv </math> |
| − | <font size=4><math> \iint(1/\sqrt{4x^2+9y^2})dA =\iint 6/\sqrt{u^2+v^2}dudv</math></font> | + | <font size=4><math> \iint(1/\sqrt{4x^2+9y^2})dA =\iint 1/6*1/\sqrt{u^2+v^2}dudv</math></font> |
Now, let's change the coordinates to polar: | Now, let's change the coordinates to polar: | ||
| − | <math> r\sin \theta = u, r\cos\theta = v, \iint 6/\sqrt{u^2+v^2}dA=\iint | + | <math> r\sin \theta = u, r\cos\theta = v, \iint 1/6\times 1/\sqrt{u^2+v^2}dA=1/6\times\iint 1/\sqrt{r^2}\times r\times drd\theta=1/6\times \int^6_0 \int^{2\pi}_0 dr d\theta=1/6\times 36\times \pi=6 pi</math> |
| + | |||
| + | ====Example #6:==== | ||
| + | Compute the following expression: | ||
| + | |||
| + | <font size=4><math> \iint(\sqrt{(x-y)(x+6y)})dA </math></font> | ||
| + | |||
| + | where dA refers to the plane bounded by the points (0,0), (1,1), (7,0),(6,-1). | ||
| + | |||
| + | ====Solution:==== | ||
| + | |||
| + | So far, we've only discussed cases where separation of variables is used to make regions easier to integrate over. For this example, separation of variables will be used to make the integrand easier. | ||
| + | |||
| + | First, let's graph the region. | ||
| + | |||
| + | [[Image:Jacobianpic5-5.png]] | ||
| + | |||
| + | As previously stated, it would relatively simple to just do the double integral with this region. However, the integrand is the real problem. And so, to make things simpler, we'll set | ||
| + | |||
| + | <font size = 4> | ||
| + | <math>u=x-y\longrightarrow \frac{\partial u}{\partial x}= 1 , \; \frac{\partial u}{\partial y} = -1</math> | ||
| + | |||
| + | <math>v=x+6y\longrightarrow \frac{\partial v}{\partial x}=1 , \; \frac{\partial v}{\partial y} =6</math> | ||
| + | |||
| + | </font> | ||
| + | Notice that in this case, we're back to substituting from the <u,v> side. | ||
| + | |||
| + | <math>J(u,v)=\begin{bmatrix} | ||
| + | \frac{\partial u}{\partial x} & \frac{\partial u}{\partial y} \\ | ||
| + | \frac{\partial v}{\partial x} & \frac{\partial v}{\partial y} \end{bmatrix}= | ||
| + | \begin{bmatrix} | ||
| + | 1 & -1 \\ | ||
| + | 1 & 6\end{bmatrix} | ||
| + | </math> | ||
| + | |||
| + | <math> dudv=\left|J(u,v)\right| \times dxdy | ||
| + | =\left|\begin{matrix} | ||
| + | 1 & -1 \\ | ||
| + | 1 & 6\end{matrix}\right|\times dxdy=(7)dxdy </math> | ||
| − | |||
| Line 235: | Line 282: | ||
In other words, if we transform a function, we can find the new tangent vector at a transformed point. | In other words, if we transform a function, we can find the new tangent vector at a transformed point. | ||
| − | ====Example # | + | ====Example #7:==== |
<math> <u,v>=<t^2,t^4>,~~~T(u,v)=<u^3-v^3,3uv>=<x,y></math> | <math> <u,v>=<t^2,t^4>,~~~T(u,v)=<u^3-v^3,3uv>=<x,y></math> | ||
| Line 284: | Line 331: | ||
Why is this important? This can help us check stability for certain systems of differential equations. | Why is this important? This can help us check stability for certain systems of differential equations. | ||
| − | ====Example # | + | ====Example #8:==== |
Find the stability of the all the critical points of | Find the stability of the all the critical points of | ||
| Line 321: | Line 368: | ||
| − | ====Example # | + | ====Example #9:==== |
Find the stability of the all the critical points of | Find the stability of the all the critical points of | ||
| Line 344: | Line 391: | ||
The eigenvalue is just 1. Since this is positive, the critical point is unstable. | The eigenvalue is just 1. Since this is positive, the critical point is unstable. | ||
| − | ====Example # | + | ====Example #10:==== |
Find the stability of the all the critical points of | Find the stability of the all the critical points of | ||
Revision as of 10:34, 10 May 2013
Contents
[hide]- 1 Jacobians and their applications
Jacobians and their applications
by Joseph Ruan, proud Member of the Math Squad.
Basic Definition
The Jacobian Matrix is just a matrix that takes the partial derivatives of each element of a transformation. In general, the Jacobian Matrix of a transformation F, looks like this:
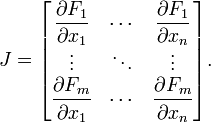 F1,F2, F3... are each of the elements of the output vector and x1,x2, x3 ... are each of the elements of the input vector.
F1,F2, F3... are each of the elements of the output vector and x1,x2, x3 ... are each of the elements of the input vector.
So for example, in a 2 dimensional case, let T be a transformation such that T(u,v)=<x,y> then the Jacobian matrix of this function would look like this:
$ J(u,v)=\begin{bmatrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \end{bmatrix} $
This Jacobian matrix noticably holds all of the partial derivatives of the transformation with respect to each of the variables. Therefore each row contains how a particular output element changes with respect to each of the input elements. This means that the Jacobian matrix contains vectors that help describe how a change in any of the input elements affects the output elements.
To help illustrate making Jacobian matrices, let's do some examples:
Example #1:
What would be the Jacobian Matrix of this Transformation?
$ T(u,v) = <u\times \cos v, u\times \sin v> $ .
Solution:
$ x=u \times \cos v \longrightarrow \frac{\partial x}{\partial u}= \cos v , \; \frac{\partial x}{\partial v} = -u\times \sin v $
$ y=u\times\sin v \longrightarrow \frac{\partial y}{\partial u}= \sin v , \; \frac{\partial y}{\partial v} = u\times \cos v $
$ J(u,v)=\begin{bmatrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \end{bmatrix}= \begin{bmatrix} \cos v & -u\times \sin v \\ \sin v & u\times \cos v \end{bmatrix} $
Example #2:
What would be the Jacobian Matrix of this Transformation?
$ T(u,v) = <u, v, u^v>,u>0 $ .
Solution:
Notice, that this matrix will not be square because there is a difference in dimensions of the input and output, i.e. the transformation is not injective.
$ x=u \longrightarrow \frac{\partial x}{\partial u}= 1 , \; \frac{\partial x}{\partial v} = 0 $
$ y=v \longrightarrow \frac{\partial y}{\partial u}=0 , \; \frac{\partial y}{\partial v} = 1 $
$ z=u^v \longrightarrow \frac{\partial y}{\partial u}= u^{v-1}\times v, \; \frac{\partial y}{\partial v} = u^v\times ln(u) $
$ J(u,v)=\begin{bmatrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \\ \frac{\partial z}{\partial u} & \frac{\partial z}{\partial v} \end{bmatrix}= \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ u^{v-1}\times v & u^v\times ln(u)\end{bmatrix} $
Example #3:
What would be the Jacobian Matrix of this Transformation?
$ T(u,v) = <\tan (uv)> $ .
Solution:
Notice, that this matrix will not be square because there is a difference in dimensions of the input and output, i.e. the transformation is not injective.
$ x=\tan(uv) \longrightarrow \frac{\partial x}{\partial u}= \sec^2(uv)\times v, \; \frac{\partial x}{\partial v} = sec^2(uv)\times u $
$ J(u,v)= \begin{bmatrix}\frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \end{bmatrix}=\begin{bmatrix}\sec^2(uv)\times v & sec^2(uv)\times u \end{bmatrix} $
Application #1: Jacobian Determinants
The determinant of Example #1 gives:
$ \left|\begin{matrix} \cos v & -u \times \sin v \\ \sin v & u \times \cos v \end{matrix}\right|=~~ u \cos^2 v + u \sin^2 v =~~ u $
Notice that, in an integral when changing from cartesian coordinates (dxdy) to polar coordinates $ (drd\theta) $, the equation is as such:
$ dxdy=r\times drd\theta=u\times dudv $
It is easy to extrapolate, then, that the transformation from one set of coordinates to another set is merely
$ dC2=det(J(T))dC1 $
where C1 is the first set of coordinates, det(J(C1)) is the determinant of the Jacobian matrix made from the Transformation T, T is the Transformation from C1 to C2 and C2 is the second set of coordinates.
It is important to notice several aspects: first, the determinant is assumed to exist and be non-zero, and therefore the Jacobian matrix must be square and invertible. This makes sense because when changing coordinates, it should be possible to change back.
Moreover, recall from linear algebra that, in a two dimensional case, the determinant of a matrix of two vectors describes the area of the parallelogram drawn by it, or more accurately, it describes the scale factor between the unit square and the area of the parallelogram. If we extend the analogy, the determinant of the Jacobian would describe some sort of scale factor change from one set of coordinates to the other. Here is a picture that should help:
This is the general idea behind change of variables. It is easy to that the jacobian method matches up with one-dimensional change of variables:
$ T(u)=\begin{matrix}u^2\end{matrix}=\begin{matrix}x\end{matrix} $ $ ~~~,~~~~~~~~ J(u)=\begin{bmatrix}\frac{\partial x}{\partial u}\end{bmatrix}=\begin{bmatrix}2u\end{bmatrix} $$ ,~~~~~~~ du=\left|J(u)\right|\times du=2u\times dx $
Remember that when substituting, to be VERY careful. If you substitute from the <x,y>= direction, then the previous formula was correct. However, if you you substitute from the <u,v>= direction, then you need to have the Jacobian on the other side. What do I mean?
it should always be the case where
$ J(\vec u) \times d\vec x = d\vec u, J(\vec x) \times d\vec u = d\vec x $.
Let's do some examples to show what I mean.
Example #4:
Compute the following expression:
$ \iint(x^2+y^2)dA $
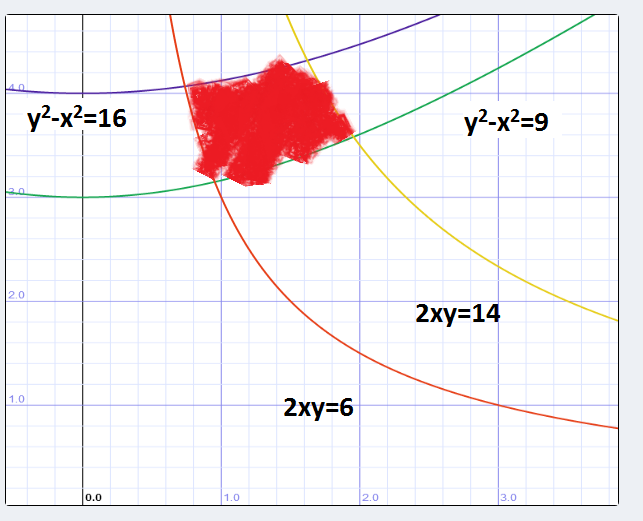
where dA is the region bounded by y2-x2=9, y2-x2=16, 2xy=14, 2xy=6.
Solution:
First, let's graph the region.
$ Let ~~~~ v=2xy, ~~~~ u=y^2-x^2 $.
Why do we do this? Let's look at the bounds: they're from y2-x2 =9 to y2 -x2=16 and 2xy=6 and 2xy=14.It'd be quite a simple task if the integral looked something like this:
$ \int^{16}_9 \int^{14}_6 k(u,v)\mathrm{d}u\mathrm{d}v $
However, notice that in this case, instead of substituting <x,y>=, we're substituting from <u,v>= perspective. This means that we will have to divide the determinant of the Jacobian from the <u,v> side instead of multiplying it.
$ u=2xy\longrightarrow \frac{\partial u}{\partial x}= 2y , \; \frac{\partial u}{\partial y} = 2x $
$ v=y^2-x^2\longrightarrow \frac{\partial v}{\partial x}= -2x , \; \frac{\partial v}{\partial y} =2y $
$ J(u,v)=\begin{bmatrix} \frac{\partial u}{\partial x} & \frac{\partial u}{\partial y} \\ \frac{\partial v}{\partial x} & \frac{\partial v}{\partial y} \end{bmatrix}= \begin{bmatrix} 2y & 2x \\ -2x & 2y\end{bmatrix} $
$ dudv= \left|J(u,v)\right|\times dxdy \longrightarrow \left|\begin{matrix} 2y & 2x \\ 2x & -2y\end{matrix}\right|\times dudv=(4y^2+4x^2)dxdy $
The new region looks like this: 
Therefore,
$ \iint(x^2+y^2)dA=\int^{16}_9 \int^{14}_6 (x^2+y^2)/(4y^2+4x^2)\mathrm{d}u\mathrm{d}v=\int^{16}_9 \int^{14}_6 1/4\mathrm{d}u\mathrm{d}v=(16-9)\times (14-6)\times 1/4=7/2. $
Example #5:
Compute the following expression:
$ \iint(1/\sqrt{4x^2+9y^2})dA $
where dA is the region bounded by (2x)2+(3y)2=36.
Solution:
Again, let's graph the region.
There are many ways to approach this, but to start, let's choose the change of variables to be x=u/2, y=v/3. Why?
$ (2x)^2+(3y)^2=36\longrightarrow u^2+v^2=36 $
The region now looks like this: 
We've turned the region from an ellipse to a circle!
Notice that in this case, we're substituting from the <x,y> side, meaning that the jacobian will be flipped.
$ x=u/2\longrightarrow \frac{\partial x}{\partial u}= 1/2 , \; \frac{\partial x}{\partial v} = 0 $
$ y=v/3\longrightarrow \frac{\partial y}{\partial u}=0 , \; \frac{\partial y}{\partial v} =1/3 $
$ J(x,y)=\begin{bmatrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \end{bmatrix}= \begin{bmatrix} 1/2 & 0 \\ 0 & 1/3\end{bmatrix} $
$ dxdy=\left|J(x,y)\right| \times dudv =\left|\begin{matrix} 1/2 & 0 \\ 0 & 1/3\end{matrix}\right|\times dudv=(1/6)dudv $
$ \iint(1/\sqrt{4x^2+9y^2})dA =\iint 1/6*1/\sqrt{u^2+v^2}dudv $
Now, let's change the coordinates to polar:
$ r\sin \theta = u, r\cos\theta = v, \iint 1/6\times 1/\sqrt{u^2+v^2}dA=1/6\times\iint 1/\sqrt{r^2}\times r\times drd\theta=1/6\times \int^6_0 \int^{2\pi}_0 dr d\theta=1/6\times 36\times \pi=6 pi $
Example #6:
Compute the following expression:
$ \iint(\sqrt{(x-y)(x+6y)})dA $
where dA refers to the plane bounded by the points (0,0), (1,1), (7,0),(6,-1).
Solution:
So far, we've only discussed cases where separation of variables is used to make regions easier to integrate over. For this example, separation of variables will be used to make the integrand easier.
First, let's graph the region.
As previously stated, it would relatively simple to just do the double integral with this region. However, the integrand is the real problem. And so, to make things simpler, we'll set
$ u=x-y\longrightarrow \frac{\partial u}{\partial x}= 1 , \; \frac{\partial u}{\partial y} = -1 $
$ v=x+6y\longrightarrow \frac{\partial v}{\partial x}=1 , \; \frac{\partial v}{\partial y} =6 $
Notice that in this case, we're back to substituting from the <u,v> side.
$ J(u,v)=\begin{bmatrix} \frac{\partial u}{\partial x} & \frac{\partial u}{\partial y} \\ \frac{\partial v}{\partial x} & \frac{\partial v}{\partial y} \end{bmatrix}= \begin{bmatrix} 1 & -1 \\ 1 & 6\end{bmatrix} $
$ dudv=\left|J(u,v)\right| \times dxdy =\left|\begin{matrix} 1 & -1 \\ 1 & 6\end{matrix}\right|\times dxdy=(7)dxdy $
Application #2: Transforming Tangent vectors
The second major application of Jacobian Matrices comes from the fact that it is made of the partial derivatives of the transformation with respect to each original element. Therefore, when a function F is transformed by a transformation T, the tangent vector of F at a point is likewise transformed by the Jacobian Matrix.
Here is a picture to illustrate this. Note: this picture was taken from etsu.edu.
In other words, if we transform a function, we can find the new tangent vector at a transformed point.
Example #7:
$ <u,v>=<t^2,t^4>,~~~T(u,v)=<u^3-v^3,3uv>=<x,y> $
Find the velocity vector of T(u,v) at t=1.
Solution:
$ x=u^3-v^3\longrightarrow \frac{\partial x}{\partial u}= 3u^2 , \; \frac{\partial x}{\partial v} = -3v^2 $
$ y=3uv\longrightarrow \frac{\partial y}{\partial u}=3v , \; \frac{\partial y}{\partial v} =3u $
$ J(u,v)=\begin{bmatrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \end{bmatrix}= \begin{bmatrix} 3u^2 & -3v^2 \\ 3v & 3u\end{bmatrix} $
$ u'(t)=\begin{bmatrix}2t\\4t^3\end{bmatrix} $
$ J(u,v)\times u'(t)=\begin{bmatrix}3u^2 & -3v^2 \\3v & 3u\end{bmatrix} \times \begin{bmatrix}2t\\4t^3\end{bmatrix}= \begin{bmatrix}3u^2\times 2t-3v^2\times 4t^3\\3v\times 2t+3u\times 4t^3\end{bmatrix}= \begin{bmatrix}3(t^2)^2\times 2t-3(t^4)^2\times 4t^3\\3(t^4)\times 2t+3(t^2)\times 4t^3\end{bmatrix}= \begin{bmatrix}6t^5-12t^{11}\\18t^5\end{bmatrix} $
Therefore at t=1, the transformed tangent vector is:
$ \begin{bmatrix}-6\\18\end{bmatrix} $
Application #3: Linearization of Systems of Differential Equations
There is one last major application of Jacobians: approximating systems of Differential equations. Let's take the general expression:
$ \vec x'=f(\vec x,t) $
Around a point, if f(x,t) is differentiable, the system can be approximated to:
$ \vec x' \approx A\vec x ,~~~~A=J(\vec x ,t_0) $
The reason this works is similar to the idea behind one dimensional differentials:
$ dy\approx f'(x)\times dx $
Why is this important? This can help us check stability for certain systems of differential equations.
Example #8:
Find the stability of the all the critical points of
$ \begin{bmatrix} x'\\ y'\\ z'\end{bmatrix}=\begin{bmatrix}z-x\\ 3/(2+x)-3y\\3y-z\end{bmatrix} $
Solution:
To find the critical points, we set x'=y'=z'=0.
$ z=x,~~~~ y=1/3x,~~~~ 3/(2+x)-x=0 \longrightarrow (x+3)(x-1)=0,~~~~ (1,1/3,1)~~~~ (-3,-1,-3) $
Now let's find the Jacobian at (1,1/3,1)
$ J(x',y',z')=\begin{bmatrix}-1 & 0 & 1\\ -3/(2+x)^2 & -3 & 0\\ 0 & 3 & -1 \end{bmatrix}=\begin{bmatrix}-1 & 0 & 1\\ -1/3 & -3 & 0\\ 0 & 3 & -1 \end{bmatrix}. $
The eigenvalues are -3.2055694304005904, -0.8972152847997048 ± 0.6654569511528134i. Since the real parts are all negative, this critical point is locally stable.
Now let's find the Jacobian at (-3,-1,-3)
$ J(x',y',z')=\begin{bmatrix}-1 & 0 & 1\\ -3/(2+x)^2 & -3 & 0\\ 0 & 3 & -1 \end{bmatrix}=\begin{bmatrix}-1 & 0 & 1\\ -3 & -3 & 0\\ 0 & 3 & -1 \end{bmatrix}. $
The eigen values are -4, -2.5 ± 1.65831i. Because all of the real parts are negative, this critical point is locally stable.
Example #9:
Find the stability of the all the critical points of
$ \begin{bmatrix} x'\\ y'\\ z'\end{bmatrix}=\begin{bmatrix}z+2y^2+x\\ y-z^{3/2}\\ \sin(z) \end{bmatrix} $
Solution:
The only critical point in this case is (0,0,0)
Now, let's do the Jacobian.
$ J(x',y',z')=\begin{bmatrix}1 & 2y & 1\\ 0 & 1 & 3/2*z^{1/2}\\ 0 & 0 & \cos(z) \end{bmatrix}=\begin{bmatrix}1 & 0 & 1\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{bmatrix}. $
The eigenvalue is just 1. Since this is positive, the critical point is unstable.
Example #10:
Find the stability of the all the critical points of
$ \begin{bmatrix} x'\\ y'\end{bmatrix}=\begin{bmatrix}y\\ -9\sin(x)-y/5\end{bmatrix} $
Solution:
for critical points, we get that
$ y=0,~~~~ x= \pi \times k, ~~~~~ k \in \mathbb{N} $
Now, let's do the Jacobian.
$ J(x',y')=\begin{bmatrix}0 & 1\\ \cos(x) & -1/5\end{bmatrix}, $
$ Case 1) :x=2\pi k\longrightarrow J(x',y')=\begin{bmatrix}0 & 1\\ 1 & -1/5\end{bmatrix} $
$ Case 2) :x=\pi+2\pi k \longrightarrow J(x',y')=\begin{bmatrix}0 & 1\\ -1 & -1/5\end{bmatrix} $
For Case 1, the eigenvalues are -1.104987562112089 and 0.904987562112089 . Therefore, those points are saddles.
For Case 2, the eigenvalues are -0.1-0.99498743710662î and -0.1+0.99498743710662î. Therefore those critical points are spiral sinks.
Since this system is 2-d, it is possible to give a phase portrait and show you that this linearized system is accurate.
Sources:
Rhea's Summer 2013 Math Squad was supported by an anonymous gift. If you enjoyed reading this tutorial, please help Rhea "help students learn" with a donation to this project. Your contribution is greatly appreciated.