m |
|||
| Line 17: | Line 17: | ||
And, both graphs put together. | And, both graphs put together. | ||
[[Image:mixed.jpg|400px|thumb|left]] | [[Image:mixed.jpg|400px|thumb|left]] | ||
| + | |||
| + | |||
| + | With all this information, we can use Bayes rule to determine if a student is African or not. Without the information about the length of the last names, the probability of a student being African would always be 0.4, but with the added feature, it becomes easier to determine the origin of the student using Bayes theorem. | ||
| + | |||
| + | For example, If we wanted to find the probability of a student being African given a last name length of 10 letters? | ||
| + | |||
| + | We can use the Bayes Rule where; | ||
| + | |||
| + | <div style="margin-left: 25em;"> | ||
| + | <math>P(x_j|\mathbf{Y})= \frac{P(\mathbf{Y}|x_j)P(x_j)}{P(\mathbf{Y})} \qquad\qquad\qquad\qquad (5)</math> | ||
| + | </div> | ||
| + | |||
| + | where | ||
| + | |||
| + | |||
| + | |||
| + | ---- | ||
| + | *[[Honors_project_1_ECE302S12|Back to Tosin's Honors Project]] | ||
| + | *[[2013 Spring ECE 302 Boutin|Back to ECE 302 Spring 2013. Prof Boutin]] | ||
| + | *[[ECE302|Back to ECE 302]] | ||
| + | |||
| + | [[Category:Honors_project]] [[Category:ECE302]] [[Category:Pattern_recognition]] | ||
Revision as of 16:29, 22 March 2013
Illustration of Bayes Rule
The last couple of essays have provided insight into the Bayesian Decision Theory, showing how conditional probabilities are used to determine the probability of a particular event given that we know the prior probabilities. For this essay, we will be looking at a real world illustration where we can use Bayes Rule to solve a problem.
Example
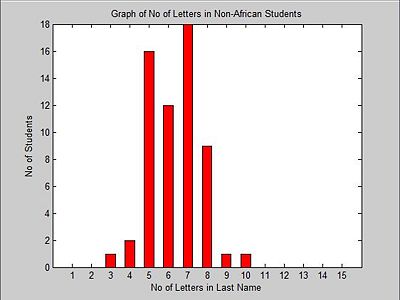
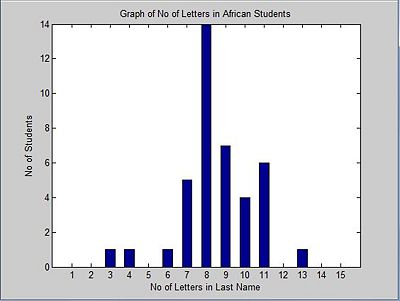
Suppose we have an ECE 302 class with 100 students, 40 African students and 60 Non-African students and we want to distinguish the students with African origin from the rest of class. Since we know that African last names are generally have long, we decide to use the number of letters in the last name as the feature to classify the students. We also have the following statistics available to us.
First, the distribution among Non-Africans.
Then the distribution among the Africans.
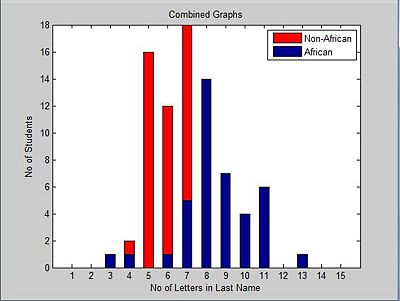
And, both graphs put together.
With all this information, we can use Bayes rule to determine if a student is African or not. Without the information about the length of the last names, the probability of a student being African would always be 0.4, but with the added feature, it becomes easier to determine the origin of the student using Bayes theorem.
For example, If we wanted to find the probability of a student being African given a last name length of 10 letters?
We can use the Bayes Rule where;
$ P(x_j|\mathbf{Y})= \frac{P(\mathbf{Y}|x_j)P(x_j)}{P(\mathbf{Y})} \qquad\qquad\qquad\qquad (5) $
where