| Line 4: | Line 4: | ||
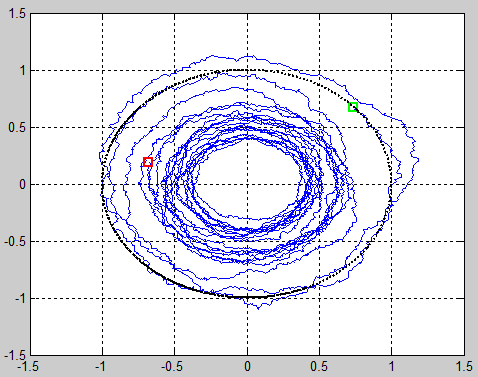
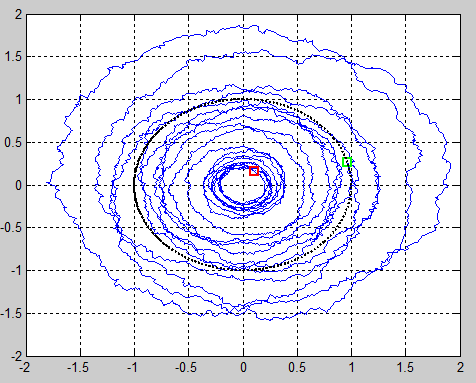
I attempted to model a robot circulating about the origin with small noise in each step. You can directly plug in the following Matlab code. It generated the following images, showing the putative robot spiraling 'inward' or 'outward'. I assume this is a result of the butterfly effect; that is, noise early in the walk process has a greater effect on the final position of the robot than noise later in the walk process. | I attempted to model a robot circulating about the origin with small noise in each step. You can directly plug in the following Matlab code. It generated the following images, showing the putative robot spiraling 'inward' or 'outward'. I assume this is a result of the butterfly effect; that is, noise early in the walk process has a greater effect on the final position of the robot than noise later in the walk process. | ||
| + | <center> | ||
[[image: Robot_1.PNG | inward spiral]] | [[image: Robot_1.PNG | inward spiral]] | ||
[[image: Robot_2.PNG | outward spiral]] | [[image: Robot_2.PNG | outward spiral]] | ||
| + | </center> | ||
<pre> | <pre> | ||
Revision as of 09:23, 16 February 2013
Markov Chains
I attempted to model a robot circulating about the origin with small noise in each step. You can directly plug in the following Matlab code. It generated the following images, showing the putative robot spiraling 'inward' or 'outward'. I assume this is a result of the butterfly effect; that is, noise early in the walk process has a greater effect on the final position of the robot than noise later in the walk process.
% set params num_steps = 10000; std_dev_rot = .01; std_dev_noise_mag = .01; % generate random initial state with complex magnitude 1 walk = zeros(1,num_steps); walk(1) = exp(i*rand); % generate next states (probabilistic modifications on current state) for j=2:length(walk), walk(j) = walk(j-1)*normrnd(1,std_noise_mag)*(i^(-abs(normrnd(0,std_rot)))); end; plot(walk); grid on; hold on; % plot starting (green) and end (red) squares plot(walk(1), 'gs','LineWidth', 2); plot(walk(length(walk)), 'rs','LineWidth', 2); % generate circle to compare with "robot" circulation circ = zeros(1,1000); circ(1) = i; for j=2:length(circ), circ(j) = circ(j-1)*i^(2*pi/length(circ)); end; plot(circ,':k','LineWidth', 2); hold off;