Difference between revisions of "ECE301 Spring2013 EC1" - Rhea

Revision as of 19:50, 10 February 2013

Convolution is often presented in a manner that emphasizes efficient calculation over comprehension of the convolution itself. To calculate in a pointwise fashion, we're told: "flip one of the input signals, and perform shift+multiply+add operations until the signals no longer overlap." This is numerically valid, but you could in fact calculate the convolution without flipping either signals (we'll do that here). Consider the convolution of the following constant input and causal impulse reponse:

$ x[n] \ast h[n] $

$ x[n] \,=\, 1 \;\;\;\;\; \forall \, n $

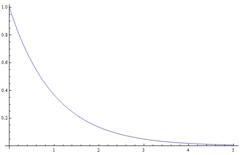
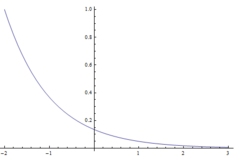
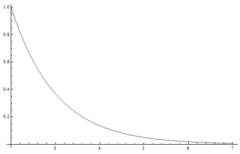
$ h[n] = \left\{ \begin{array}{lr} \mathrm{e}^{-n} & : n \geq 0\\ 0 & : n < 0 \end{array} \right. $

$ \int_{-\infty}^{\infty} h(\tau)\,\mathrm{d}\tau \,=\, \int_{0}^{\infty} h(\tau)\,\mathrm{d}\tau \;\;\;\;\; \because h(t)=0 \;\;\; \forall \, t<0 $

$ \Rightarrow \int_{0}^{\infty} \mathrm{e}^{-\tau}\,\mathrm{d}\tau \,=\, \left.-\mathrm{e}^{-\tau}\right|_{0}^{\infty} \,=\, -(\mathrm{e}^{-\infty} - \mathrm{e}^{0}) \,=\, -(0 - 1) \,=\, 1 $

$ \int_{-\infty}^{\infty} h(t-\tau)\,\mathrm{d}\tau \,=\, \int_{-\infty}^{t} h(t-\tau)\,\mathrm{d}\tau \;\;\;\;\; \because h(t)=0 \;\;\; \forall \, t<0 $

$ \Rightarrow \int_{-\infty}^{t} \mathrm{e}^{-(t-\tau)}\,\mathrm{d}\tau \,=\, \int_{-\infty}^{t} \mathrm{e}^{\tau-t}\,\mathrm{d}\tau \,=\, \left.\mathrm{e}^{\tau-t}\right|_{-\infty}^{t} \,=\, \mathrm{e}^{0} - \mathrm{e}^{-\infty-t} \;\; (\forall \, t>0) \,=\, 1 - 0 \,=\, 1 $