Difference between revisions of "Coloring problems MA375S12Walther" - Rhea

Revision as of 11:41, 16 April 2012

Coloring problems

We learned some coloring problems at the end of this semester. Graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints.We have learned vertex coloring, edges coloring, the chromatic function about coloring, deletion/contraction etc. Here I want to share several well-known coloring problems.

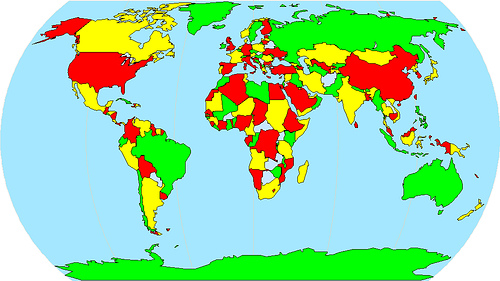
The Four-Color problem

The Four-Color Conjecture was settled in the XIX century:Every map can be colored using at most four colors in such a way that adjacent regions (i.e. those sharing a common boundary segment, not just a point) receive different colors. Clearly a graph can be constructed from any map, the regions being represented by the vertices of the graph and two vertices being joined by an edge if the regions corresponding to the vertices are adjacent. The resulting graph is planar, that is, it can be drawn in the plane without any edges crossing. So, the Four-Color Conjecture asks if the vertices of a planar graph can be colored with at most 4 colors so that no two adjacent vertices use the same color.

History

The first published reference is found in Arthur Cayley’s, On the colorings of maps, Proc. Royal Geographical Society 1, 259–261, 1879. On 17 July 1879 Alfred Bray Kempe announced in Nature that he had a proof of the Four-Color Conjecture. Kempe was a London barrister who had studied mathematics under Cayley at Cambridge and devoted some of his time to mathematics throughout his life. At Cayley’s suggestion Kempe submitted the Theorem to the American Journal of Mathematics where it was published in the ends of 1879.

Cayley Kepme

Idea of Kempe’s proof

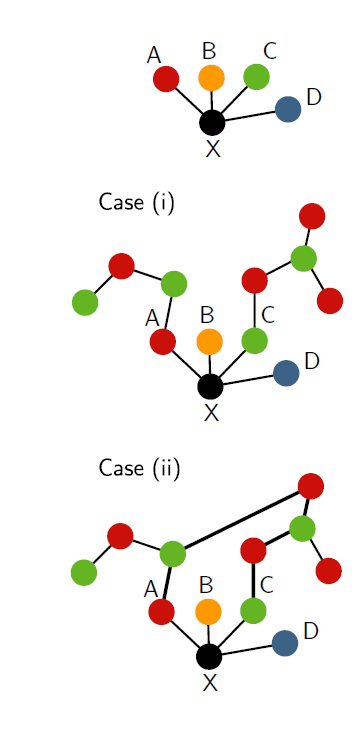
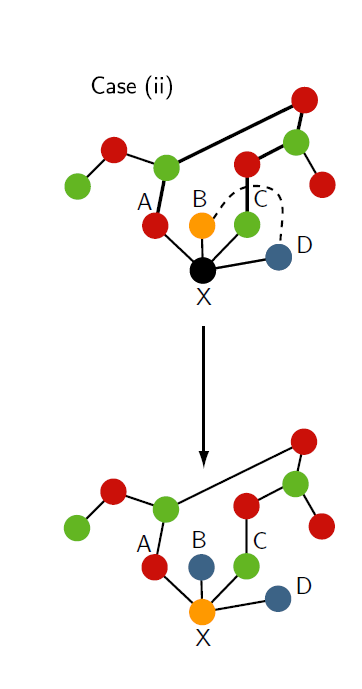
Kempe used an argument known as the method of Kempe chains. If we have a map in which every region is colored red, green, blue or yellow except one, say X. If this final region X is not surrounded by regions of all four colors there is a color left for X.

Hence suppose that regions of all four colors surround X.

If X is surrounded by regions A, B, C, D in order, colored red, yellow, green and blue then there are two cases to consider. (i) There is no chain of adjacent regions from A to C alternately colored red and green. (ii) There is a chain of adjacent regions from A to C alternately colored red and green. If (i) holds there is no problem. Change A to green, and then interchange the color of the red/green regions in the chain joining A. Since C is not in the chain it remains green and there is now no red region adjacent to X. Color X red. If (ii) holds then there can be no chain of yellow/blue adjacent regions from B to D. [It could not cross the chain of red/green regions.] Hence property (i) holds for B and D and we change colors as above.

sources from [www.ic.uff.br/elavio/mini2.pdf]

Deletion/Contraction

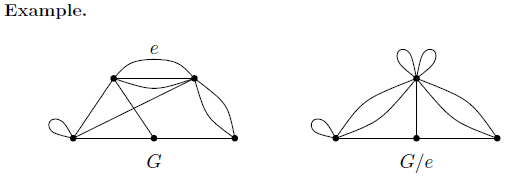
Many basic invariants associated with G can be expressed using a recurrence formula involving deletions and contractions of the edges of G. Deleting an edge

For a graph G and e ∈ E, denote by G\e the graph obtained from G by deleting e.

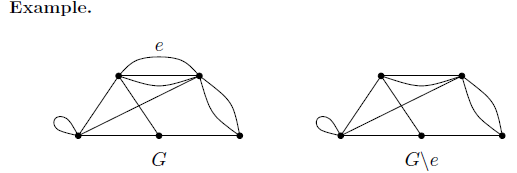
Contracting an edge

For a graph G and e ∈ E, denote by G/e the graph obtained from G by contracting e; that is, by identifying the ends of e and then deleting e.

In the class, we learned about the "Deletion/Contraction formula" which is denoted to

$ x_G=n*(n-1)*(n-2)^2 $

Furthermore, the properties of $ x_G(n) $ is:

$ x_G(n)=a_v*n^v+a_v-1*n^v-1+...+a_1*n+a_0 $ with $ a_v=1 $, the coefficient altemate in sign, and $ a_0=0 $

So here, I want to introduce something else. Is is called Deletion–contraction trees and Deletion-contraction recurrence.

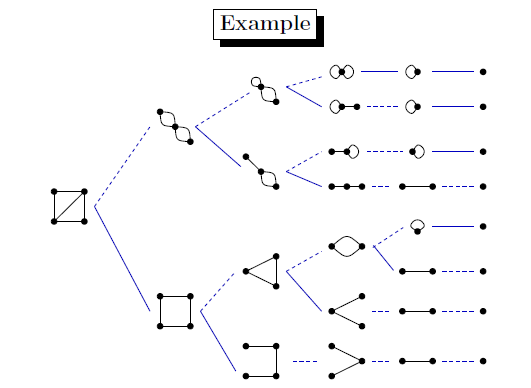
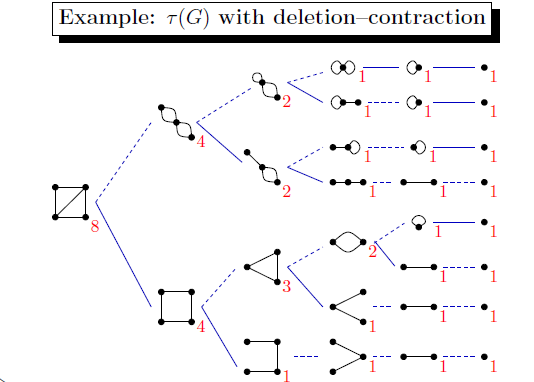
Deletion–contraction trees

Given a graph G, construct a deletion–contraction tree of G recursively as follows. The root of the tree is the graph G. If G has no edges, stop. If all edges of G are loops, and there is a loop e, recursively add the tree of G\e as a child of G. Otherwise, if G all edges of G are either loops or cut-edges, and there is a cut edge e, recursively add the tree of G/e as a child of G. Otherwise, let e be an edge that is neither a loop nor a cut-edge, recursively add the trees of G\e and G/e as children of G.

Deletion–contraction recurrences

Let f be a graph invariant. A deletion–contraction recurrence for f expresses f(G) for a nonempty G in terms of the deletion f(G\e) and the contraction f(G/e) of an edge e ∈ E. Loops and cut-edges are typically treated as special cases.

An example: spanning trees

Denote by T(G) the number of spanning trees of G. Theorem A.42 Let G be a connected graph. Then, for all e ∈ E,

(G) =1 if G has no edges;
    =T(G\e) if e is a loop;
    =T(G/e) if e is a cut-edge;
    =T(G\e) + T(G/e) otherwise.

sources from [www.tcs.hut.fi/Studies/T-79.5203/2008SPR/slides-a5.pdf]