| Line 1: | Line 1: | ||
= Video Tutorial on Convolution (aka Black Magic) = | = Video Tutorial on Convolution (aka Black Magic) = | ||
| − | + | [http://milebuddy.net/Sachin Videos on the graphical approach to convolution, and splitting during convolution.] | |
| + | |||
| + | Thanks to my homeslice Bert Haake for use of his webcam and laptop to produce the videos. | ||
| + | |||
| − | |||
In the meantime, while I was poking around Wikipedia, I found this gif online and it helps me visualize the graphical approach to convolution. If you really want to play around with this concept I have also found a sample [https://www.projectrhea.org/rhea/index.php/VideoTutorialConvolutionMATLABCodeExample MATLAB code] which can be a little fun to tweak. | In the meantime, while I was poking around Wikipedia, I found this gif online and it helps me visualize the graphical approach to convolution. If you really want to play around with this concept I have also found a sample [https://www.projectrhea.org/rhea/index.php/VideoTutorialConvolutionMATLABCodeExample MATLAB code] which can be a little fun to tweak. | ||
| Line 9: | Line 11: | ||
[[Image:Convolution of box signal with itself2.gif]] | [[Image:Convolution of box signal with itself2.gif]] | ||
| − | Basically I plan on showing this idea in my video, so until it is made I will type out my explination for it. Sorry, I know not cool. | + | Basically I plan on showing this idea in my video, so until it is made I will type out my explination for it. Sorry, I know not cool. |
| − | Here you can see that the value of the convolution at a point, t, is the area shared by the two graphs when one is centered at the origin and the other at t. One subtlety that is lost here is that one the signal being moved is flipped. Since it is symmetric it looks the same. If you look at the equation for convolution | + | Here you can see that the value of the convolution at a point, t, is the area shared by the two graphs when one is centered at the origin and the other at t. One subtlety that is lost here is that one the signal being moved is flipped. Since it is symmetric it looks the same. If you look at the equation for convolution <math>y(t)=x(t)*h(t)=\int_{-\infty}^{\infty} x(\tau)h(t-\tau) d\tau</math> <br> I will rewrite this as<br> <math>y(t)=x(t)*h(t)=\int_{-\infty}^{\infty} x(\tau)h(-\tau+t) d\tau</math> <br> You will see there is the <span class="texhtml">''x''(τ)</span> term that in the visual example is the signal centered around the origin. You will then see there is <span class="texhtml">''h''( − τ + ''t'')</span> term. If we think about what this means it is the graph of the second signal flipped (the negative tau) and centered around t (the +t). So as we change t we change the location of this function and thus the amount of overlapped area, which is calculated by the integral.<br><br> |
| − | <math>y(t)=x(t)*h(t)=\int_{-\infty}^{\infty} x(\tau)h(t-\tau) d\tau</math> <br> | + | |
| − | I will rewrite this as<br> | + | |
| − | <math>y(t)=x(t)*h(t)=\int_{-\infty}^{\infty} x(\tau)h(-\tau+t) d\tau</math> <br> | + | |
| − | You will see there is the < | + | |
| − | You will then see there is < | + | |
| − | The convolution is the graph of each of these overlapped areas vs. t. | + | The convolution is the graph of each of these overlapped areas vs. t. <br> --[[User:Ssanthak|Ssanthak]] 23:03, 5 May 2011 (UTC) |
| − | <br> --[[User:Ssanthak|Ssanthak]] 23:03, 5 May 2011 (UTC) | + | |
Revision as of 09:54, 6 May 2011
Video Tutorial on Convolution (aka Black Magic)
Videos on the graphical approach to convolution, and splitting during convolution.
Thanks to my homeslice Bert Haake for use of his webcam and laptop to produce the videos.
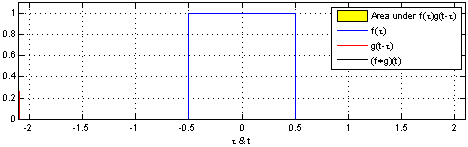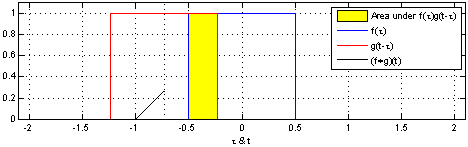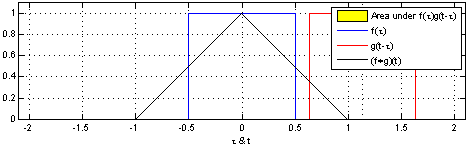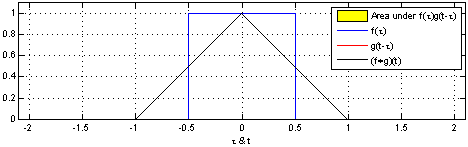
In the meantime, while I was poking around Wikipedia, I found this gif online and it helps me visualize the graphical approach to convolution. If you really want to play around with this concept I have also found a sample MATLAB code which can be a little fun to tweak.
Basically I plan on showing this idea in my video, so until it is made I will type out my explination for it. Sorry, I know not cool.
Here you can see that the value of the convolution at a point, t, is the area shared by the two graphs when one is centered at the origin and the other at t. One subtlety that is lost here is that one the signal being moved is flipped. Since it is symmetric it looks the same. If you look at the equation for convolution $ y(t)=x(t)*h(t)=\int_{-\infty}^{\infty} x(\tau)h(t-\tau) d\tau $
I will rewrite this as
$ y(t)=x(t)*h(t)=\int_{-\infty}^{\infty} x(\tau)h(-\tau+t) d\tau $
You will see there is the x(τ) term that in the visual example is the signal centered around the origin. You will then see there is h( − τ + t) term. If we think about what this means it is the graph of the second signal flipped (the negative tau) and centered around t (the +t). So as we change t we change the location of this function and thus the amount of overlapped area, which is calculated by the integral.
The convolution is the graph of each of these overlapped areas vs. t.
--Ssanthak 23:03, 5 May 2011 (UTC)