m |
|||
| Line 176: | Line 176: | ||
<math>y_1[n]= \frac{x[n]+x[n-1]}{2} </math><br> | <math>y_1[n]= \frac{x[n]+x[n-1]}{2} </math><br> | ||
| − | Applying Z-transform on both sides and grouping terms, we can obtain the transfer function<br> | + | Applying Z-transform on both sides and grouping terms, we can obtain the transfer function<br/> |
<math>\begin{align} | <math>\begin{align} | ||
| Line 211: | Line 211: | ||
---- | ---- | ||
| − | <math>y_3[n]= \frac{x[n+1]+x[n]+x[n-1]}{3} </math><br> Applying Z-transform on both sides and grouping terms, we can obtain the transfer function<br> | + | <math>y_3[n]= \frac{x[n+1]+x[n]+x[n-1]}{3} </math><br/> |
| + | Applying Z-transform on both sides and grouping terms, we can obtain the transfer function<br/> | ||
<math>\begin{align} | <math>\begin{align} | ||
| Line 228: | Line 229: | ||
---- | ---- | ||
| − | <math>y_4[n]= \frac{x[n+1]-2 x[n]+x[n-1]}{4}. </math> Applying Z-transform on both sides and grouping terms, we can obtain the transfer function<br> | + | <math>y_4[n]= \frac{x[n+1]-2 x[n]+x[n-1]}{4}. </math><br/> |
| + | Applying Z-transform on both sides and grouping terms, we can obtain the transfer function<br/> | ||
<math>\begin{align} | <math>\begin{align} | ||
Revision as of 20:28, 2 November 2010
Solution to HW7
Q1.
Recall, the Discrete Fourier Transform is defined as follows -
Definition: let x[n] be a DT signal with Period N. Then,
$ X [k] = \sum_{k=0}^{N-1} x[n].e^{-j2\pi kn/N} $
$ x [n] = (1/N) \sum_{k=0}^{N-1} X[k].e^{j2\pi kn/N} $
What is the relation between the DFT and the Fourier series coefficients of continuous periodic function x[n]?
The DFT of a sampled signal x[n] of length N is directly proportional to the Fourier series coefficients of the continuous periodic version of x[n].
The DFT of the N samples comprising one period of x[n] equals N times the Fourier series coefficients.
Alternatively -
The fourier series coefficients of a periodic, bandlimited signal x are given by the DFT of one period of the samples of x, divided by N, where N is the DFT length and N is also the number of samples in each period of x.
Credit: Julius Smith III, stanford.edu
$ x_1[n]= e^{j \frac{2}{3} \pi n}; $
Function's period N = 3,
Using IDFT,
$ \begin{align} x_1[n] &= \frac{1}{3} \sum_{k=0}^{2} X[k].e^{j2\pi kn/3} \\ e^{j \frac{2}{3} \pi n} &= \frac{1}{3} \sum_{k=0}^{2} X[k].e^{j2\pi kn/3} \\ &= \frac{1}{3} \left[ X[0].e^{j0} + X[1].e^{j2\pi n/3} + X[2].e^{j2\pi n(2/3)} \right] \\ &= \frac{1}{3} \left[ X[0] + X[1].e^{j2\pi n/3} + X[2].e^{j4\pi n/3} \right] \end{align} $
For the two sides to be equal,
X[0] = 0
X[1] = 3
X[2] = 0
Plugging in we can verify,
$ \begin{align} e^{j \frac{2}{3} \pi n} &= \frac{1}{3} \left[ 0 + 3.e^{j2\pi n/3} + 0 \right]\\ e^{j \frac{2}{3} \pi n} &= \frac{1}{3} 3.e^{j2\pi n/3} \\ e^{j \frac{2}{3} \pi n} &= e^{j \frac{2}{3} \pi n} \end{align} $
So our three selected values for X[k] are correct. Thus
$ X[k] = \begin{cases} 3, & k = 1 \\ 0, & \mbox{else} \end{cases} $
$ x_2[n]= e^{j \frac{2}{\sqrt{3}} \pi n}; $
Function x2[n] is aperiodic. Let's see why -
Assume x2[n] is periodic, then
$ e^{j \frac{2}{\sqrt{3}} \pi n} = e^{j \frac{2}{\sqrt{3}} \pi (n + N)} $ for function to be periodic, where N is an integer
$ e^{j \frac{2}{\sqrt{3}} \pi n} = e^{j \frac{2}{\sqrt{3}} \pi n}e^{j \frac{2}{\sqrt{3}} \pi N} $
$ e^{j \frac{2}{\sqrt{3}} \pi n} = e^{j \frac{2}{\sqrt{3}} \pi n}.(1) $
$ e^{j \frac{2}{\sqrt{3}} \pi N} = 1 $
For this to be true -
$ j \frac{2}{\sqrt{3}} \pi N = j 2\pi n, $ where n is an integer
$ N = n\sqrt{3} $
N is not an integer and this contradicts our assumption, proving that it cannot be true.
Thus, x_2[n] is aperiodic and we cannot apply the DFT.
$ x_3[n]= e^{j \frac{4}{3} \pi n}; $
Function's period N = 3,
Using IDFT,
$ \begin{align} x_3[n] &= \frac{1}{3} \sum_{k=0}^{2} X[k].e^{j2\pi kn/3} \\ e^{j \frac{4}{3} \pi n} &= \frac{1}{3} \sum_{k=0}^{2} X[k].e^{j2\pi kn/3} \\ &= \frac{1}{3} \left[ X[0].e^{j0} + X[1].e^{j2\pi n/3} + X[2].e^{j2\pi n(2/3)} \right] \\ &= \frac{1}{3} \left[ X[0] + X[1].e^{j2\pi n/3} + X[2].e^{j4\pi n/3} \right] \end{align} $
For the two sides to be equal,
X[0] = 0
X[1] = 0
X[2] = 3
$ X[k] = \begin{cases} 3, & k = 2 \\ 0, & \mbox{else} \end{cases} $
$ x_4[n]= e^{j \frac{2}{1000} \pi n}; $ Function's period N = 1000,
Using IDFT,
$ \begin{align} x_4[n] &= \frac{1}{1000} \sum_{k=0}^{999} X[k].e^{j2\pi kn/1000} \\ e^{j \frac{2}{1000} \pi n} &= \frac{1}{1000} \sum_{k=0}^{999} X[k].e^{j2\pi kn/1000} \\ &= \frac{1}{1000} \left[ X[0].e^{j0} + X[1].e^{j2\pi n/1000} + X[2].e^{j2\pi n(2/1000)} + ... \right] \\ &= \frac{1}{1000} \left[ X[0] + X[1].e^{j2\pi n/1000} + X[2].e^{j4\pi n/1000} + ... \right] \end{align} $
For the two sides to be equal,
X[0] = 0
X[1] = 1000
X[2] = 0
$ X[k] = \begin{cases} 1000, & k = 1 \\ 0, & \mbox{else} \end{cases} $
$ x_5[n]= e^{-j \frac{2}{1000} \pi n}; $ Function's period N = 1000,
$ \begin{align} x_5[n]&= e^{-j \frac{2}{1000} \pi n}.1 \\ &= e^{-j \frac{2}{1000} \pi n}.e^{-j 2\pi n} \\ &= e^{j 2\pi n(1 - (1/1000))} \\ &= e^{j 2\pi n\frac{999}{1000} } \\ \end{align} $
Using IDFT,
$ \begin{align} x_5[n] &= \frac{1}{1000} \sum_{k=0}^{999} X[k].e^{j2\pi kn/1000} \\ e^{j 2\pi n\frac{999}{1000}} &= \frac{1}{1000} \sum_{k=0}^{999} X[k].e^{j2\pi kn/1000} \\ &= \frac{1}{1000} \left[ X[0].e^{j0} + X[1].e^{j2\pi n/1000} + X[2].e^{j2\pi n(2/1000)}+ ... + X[999].e^{j2\pi n(999/1000)} \right] \\ &= \frac{1}{1000} \left[ X[0] + X[1].e^{j2\pi n/1000} + X[2].e^{j2\pi n (2/1000)} + ... + X[999].e^{j2\pi n(999/1000)} \right] \\ \end{align} $
For the two sides to be equal,
X[0] = 0
X[1] = 0
X[2] = 0
X[999] = 1000
$ X[k] = \begin{cases} 1000, & k = 999 \\ 0, & \mbox{else} \end{cases} $
$ \begin{align} x_6[n] &= \cos\left( \frac{2}{1000} \pi n\right) \\ &= \frac{1}{2}\left( e^{j\frac{2\pi n}{1000}} + e^{-j\frac{2\pi n}{1000}} \right) \\ &= \frac{1}{2} (x_4[n] + x_5[n]) \\ \end{align} $
We have an additional (1/2) to factor into the final coefficients, giving us -
$ X[k] = \begin{cases} 500, & k = 1 \\ 500, & k = 999 \\ 0, & \mbox{else} \end{cases} $
$ \begin{align} x_7[n] &= \cos^2\left( \frac{2}{1000} \pi n\right) \\ &= \left[ \frac{1}{2}\left( e^{j\frac{2\pi n}{1000}} + e^{-j\frac{2\pi n}{1000}} \right)\right]^2 \\ &= \frac{1}{4}\left( e^{j\frac{4\pi n}{1000}} + 2 + e^{-j\frac{4\pi n}{1000}} \right) \\ &= \frac{1}{4}\left( 2 + e^{j2\pi n\frac{2}{1000}} + e^{-j2\pi n\frac{2}{1000}}e^{-j2\pi n} \right) \\ &= \frac{1}{4}\left( 2 + e^{j2\pi n\frac{2}{1000}} + e^{j2\pi n\frac{998}{1000}} \right) \\ \end{align} $
Function's period N = 1000,
Using IDFT,
$ \begin{align} x_7[n] &= \frac{1}{1000} \sum_{k=0}^{999} X[k].e^{j2\pi kn/1000} \\ &= \frac{1}{1000} \left[ X[0] + X[1].e^{j2\pi n/1000} + X[2].e^{j2\pi n(2/1000)} + ... X[998].e^{j2\pi n(998/1000)} + X[999].e^{j2\pi n(999/1000)} \right] \\ \end{align} $
Comparing LHS and RHS,
X[0] = 2000
X[1] = 0
X[2] = 250
...
X[998] = 250
X[999] = 0
$ X[k] = \begin{cases} 2000, & k = 0 \\ 250, & k = 2 \\ 250, & k = 998 \\ 0, & \mbox{else} \end{cases} $
$ \begin{align} x_8[n]= (-j)^n \\ &= (e^{j \pi /2})^n \\ &= e^{j \pi n/2} \\ \end{align} $
Function's period N = 4,
Using IDFT,
$ \begin{align} x_8[n] &= \frac{1}{4} \sum_{k=0}^{3} X[k].e^{j2\pi kn/4} \\ e^{j \pi n/2} &= \frac{1}{4} \sum_{k=0}^{3} X[k].e^{j2\pi kn/4} \\ &= \frac{1}{4} \left[ X[0].e^{j0} + X[1].e^{j2\pi n/4} + X[2].e^{j2\pi n(2/4)} + X[3].e^{j2\pi n(3/4)}\right] \\ &= \frac{1}{4} \left[ X[0] + X[1].e^{j\pi n/2} + X[2].e^{j\pi n} + X[3].e^{j\pi n(3/2)} \right] \end{align} $
For the two sides to be equal,
X[0] = 0
X[1] = 4
X[2] = 0
X[2] = 0
$ X[k] = \begin{cases} 4, & k = 1 \\ 0, & \mbox{else} \end{cases} $
Q2.
$ y_1[n]= \frac{x[n]+x[n-1]}{2} $
Applying Z-transform on both sides and grouping terms, we can obtain the transfer function
$ \begin{align} Y_1[z]&= \frac{X[z]+X[z].z^{-1}}{2} \\ \frac{Y_1[z]}{X[z]}&= \frac{1+z^{-1}}{2} \\ H_1[z] &= \frac{1+z^{-1}}{2} \\ \end{align} $
Frequency Response H_1(ω),
$ \begin{align} H_1[e^{j\omega }] &= \frac{1+e^{-j\omega }}{2} \\ &= e^{-j\frac{\omega }{2}} \left( \frac{e^{j\frac{\omega }{2}}+e^{-j\frac{\omega }{2}}}{2} \right) \\ &= e^{-j\frac{\omega }{2}} cos \left( \frac{\omega }{2} \right) \\ \end{align} $
$ y_2[n]= \frac{x[n]-x[n-1]}{2} $
Applying Z-transform on both sides and grouping terms, we can obtain the transfer function
$ \begin{align} Y_2[z]&= \frac{X[z]-X[z].z^{-1}}{2} \\ \frac{Y_2[z]}{X[z]}&= \frac{1-z^{-1}}{2} \\ H_2[z] &= \frac{1-z^{-1}}{2} \\ \end{align} $
Frequency Response H_2(ω),
$ \begin{align} H_2[e^{j\omega }] &= \frac{1-e^{-j\omega }}{2} \\ &= e^{-j\frac{\omega }{2}} \left( \frac{e^{j\frac{\omega }{2}}-e^{-j\frac{\omega }{2}}}{2} \right) \\ &= je^{-j\frac{\omega }{2}} \left( \frac{e^{j\frac{\omega }{2}}-e^{-j\frac{\omega }{2}}}{2j} \right) \\ &= je^{-j\frac{\omega }{2}} sin \left( \frac{\omega }{2} \right) \\ \end{align} $
$ y_3[n]= \frac{x[n+1]+x[n]+x[n-1]}{3} $
Applying Z-transform on both sides and grouping terms, we can obtain the transfer function
$ \begin{align} Y_3[z]&= \frac{X[z].z+ X[z] + X[z].z^{-1}}{3} \\ \frac{Y_3[z]}{X[z]}&= \frac{z(1+z^{-1} + z^{-2})}{3} \\ H_3[z] &= \frac{1+z^{-1} + z^{-2}}{3z^{-1}} \\ \end{align} $
Frequency Response H_3(ω),
$ \begin{align} H_3[e^{j\omega }] &= \frac{1+e^{-j\omega }+e^{-j2\omega }}{3e^{-j\omega }} \\ &= \frac{e^{-j\omega }+e^{-j\omega }(e^{j\omega } + e^{-j\omega })}{3e^{-j\omega }} \\ &= \frac{e^{-j\omega }(1+2cos(\omega ))}{3e^{-j\omega }} \\ &= \frac{1+2cos(\omega )}{3} \\ \end{align} $
$ y_4[n]= \frac{x[n+1]-2 x[n]+x[n-1]}{4}. $
Applying Z-transform on both sides and grouping terms, we can obtain the transfer function
$ \begin{align} Y_4[z]&= \frac{X[z].z- 2X[z] + X[z].z^{-1}}{4} \\ \frac{Y_3[z]}{X[z]}&= \frac{z(1-2z^{-1} + z^{-2})}{4} \\ H_3[z] &= \frac{1-2z^{-1} + z^{-2}}{4z^{-1}} \\ \end{align} $
Frequency Response H_3(ω),
$ \begin{align} H_4[e^{j\omega }] &= \frac{1-2e^{-j\omega }+e^{-j2\omega }}{4e^{-j\omega }} \\ &= \frac{-2e^{-j\omega }+ 2 e^{-j\omega }\frac{(e^{j\omega } + e^{-j\omega })}{2}}{4e^{-j\omega }} \\ &= \frac{2e^{-j\omega }(cos(\omega )-1)}{4e^{-j\omega }} \\ &= \frac{cos(\omega )-1}{2} \\ \end{align} $
Q3.
a. Substituting values directly would yield the following -
$ \begin{align} n &= ...\text{ -3, -2, -1, 0, 1, 2, 3, 4, 5} ...\\ y\left[n\right] &= ...\text{ 0, -2, -4, -1, 2, -1, -4, -2, 0} ...\\ \end{align} $
b. h[n] = ?
Substitute x[n] = δ[n] to obtain y[n] = h[n],
h[n] = δ[n] + 2δ[n − 1] + δ[n − 2]
Now x[n] = -2δ[n + 2] + δ[n] - 2δ[n − 2]
$ \begin{align} y[n] &= x[n] * h[n] \\ &= (-2\delta[n+2] + \delta[n] - 2\delta[n-2]) * (\delta[n] + 2\delta[n-1] + \delta[n-2]) \\ &= -2\delta[n+2] - 4\delta[n+1] -2\delta[n] + \delta[n] + 2\delta[n-1] + \delta[n-2] - 2\delta[n-2] - 4\delta[n-3] - 2\delta[n-4] \\ &= -2\delta[n+2] - 4\delta[n+1] - \delta[n] + 2\delta[n-1] - \delta[n-2] - 4\delta[n-3] = 2\delta[n-4] \\ \end{align} $
c. x[n] = ejωn
(i)
$ \begin{align} y[n] &= e^{j\omega n} + 2 e^{j\omega (n-1)} + e^{j\omega (n-2)} \\ &= e^{j\omega n}(1 + 2 e^{-j\omega } + e^{-2j\omega }) \\ H(e^{j\omega}) &= 1 + 2 e^{-j\omega } + e^{-2j\omega } \\ \end{align} $
(ii)
h[n] = δ[n] + 2δ[n − 1] + δ[n − 2]
H(ejω) = 1 + 2 e − jω + e − 2jω
(i) and (ii) are the same.
d. x[n] = -2δ[n + 2] + δ[n] - 2δ[n − 2]
X(ejω) = -2 e2jω + 1 - 2e − 2jω
$ \begin{align} Y(e^{j\omega}) &= X(e^{j\omega})H(e^{j\omega}) \\ &= (-2e^{2j\omega } + 1 - 2e^{-2j\omega } ).(1 + 2e^{-j\omega } + e^{-2j\omega }) \\ &= -2e^{2j\omega } - 4e^{j\omega } - 2 + 1 + 2e^{-j\omega } + 2e^{-2j\omega } - 2e^{-2j\omega } - 4e^{-3j\omega } - 2e^{-4j\omega } \\ &= -2e^{2j\omega } - 4e^{j\omega } - 1 - 2e^{-j\omega } - e^{-2j\omega } - 4e^{-3j\omega } - 2e^{-4j\omega } \\ \\ \text{Using Inverse DTFT,} \\ y[n] &= -2\delta[n+2] - 4\delta[n+1] - \delta[n] + 2\delta[n-1] - \delta[n-2] - 4\delta[n-3] - 2\delta[n-4] \\ \end{align} $
All 3 approaches lead to the same y[n].
Q4. $ H(z)= \frac{1-\frac{1}{2}z^{-2}} {1-\frac{1}{\sqrt{2}} z^{-1} +\frac{1}{4} z^{-2}} $
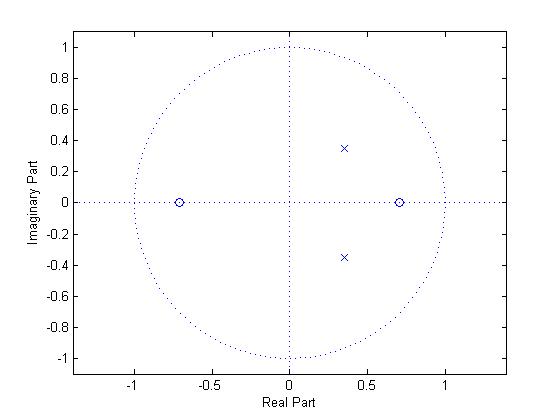
- a. Sketch the locations of the poles and zeros.
$ \begin{align} H(z) &= \frac{1-\frac{1}{2}z^{-2}}{1-\frac{1}{\sqrt{2}} z^{-1} +\frac{1}{4} z^{-2}} \\ H(z) &= \frac{(z+\frac{1}{\sqrt{2}})(z-\frac{1}{\sqrt{2}})} { (z-(\frac{1}{2\sqrt{2}} + j\frac{1}{2\sqrt{2}}))(z-(\frac{1}{2\sqrt{2}} - j\frac{1}{2\sqrt{2}})) } \\ \end{align} $
Zeros:
$ z_1 = \frac{1}{\sqrt{2}}, z_2 = -\frac{1}{\sqrt{2}} $
Poles:
$ p_1 = \frac{1}{2\sqrt{2}} + j\frac{1}{2\sqrt{2}}, p_2 = \frac{1}{2\sqrt{2}} - j\frac{1}{2\sqrt{2}} $
- b. Determine the magnitude and phase of the frequency response H(ω), for
$ \omega = 0 $
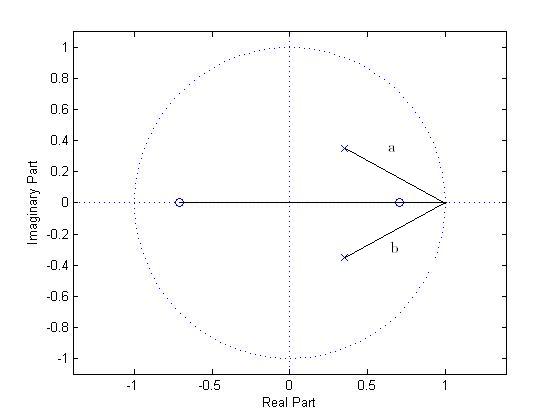 $ \left| H(e^{j\omega}) \right| = \left| H(e^{j0}) \right| = \left| H(z=1) \right| $
$ \left| H(e^{j\omega}) \right| = \left| H(e^{j0}) \right| = \left| H(z=1) \right| $
$ = \left| \frac{(1+\frac{1}{\sqrt{2}})(1-\frac{1}{\sqrt{2}})} { (1-(\frac{1}{2\sqrt{2}} + j\frac{1}{2\sqrt{2}}))(1-(\frac{1}{2\sqrt{2}} - j\frac{1}{2\sqrt{2}})) } \right| = 0.921 $
$ \angle H(e^{j0}) = \angle c + \angle d - \angle a - \angle b = 0 $
$ \omega =\frac{\pi}{4} $
$ = \left| \frac{(\frac{1}{\sqrt{2}} + j\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}})(\frac{1}{\sqrt{2}} + j\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}})} { (\frac{1}{\sqrt{2}} + j\frac{1}{\sqrt{2}}-(\frac{1}{\sqrt{2}} + j\frac{1}{\sqrt{2}}))(\frac{1}{\sqrt{2}} + j\frac{1}{\sqrt{2}}-(\frac{1}{\sqrt{2}} - j\frac{1}{\sqrt{2}})) } \right| = 0 $
$ \angle H(e^{j\frac{\pi}{4}}) = \angle c + \angle d - \angle a - \angle b = \frac{\pi}{2} + arctan^{-1} \left( \frac{\frac{1}{\sqrt{2}}}{\sqrt{2}} \right) - \frac{\pi}{2} - arctan^{-1} \left( \frac{\frac{1}{\sqrt{2}} + \frac{1}{2\sqrt{2}}}{1-\sqrt{2}-\frac{1}{2\sqrt{2}}} \right) = 0 $
$ \omega =\frac{\pi}{2} $
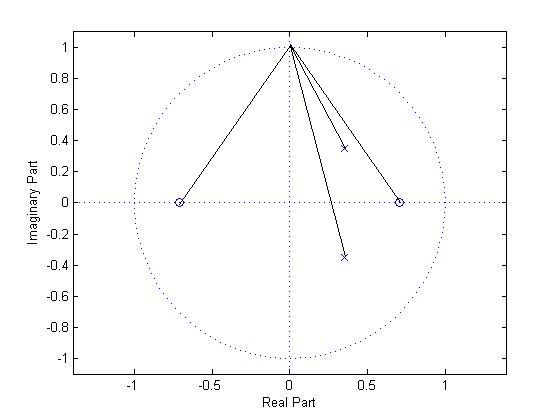 $ \left| H(e^{j\omega}) \right| = \left| H(e^{j\frac{\pi}{2}}) \right| = \left| H(z=j) \right| $
$ \left| H(e^{j\omega}) \right| = \left| H(e^{j\frac{\pi}{2}}) \right| = \left| H(z=j) \right| $
$ = \left| \frac{(j+\frac{1}{\sqrt{2}})(j-\frac{1}{\sqrt{2}})} { (j-(\frac{1}{2\sqrt{2}} + j\frac{1}{2\sqrt{2}}))(j-(\frac{1}{2\sqrt{2}} - j\frac{1}{2\sqrt{2}})) } \right| = 1.455 $
$ \angle H(e^{j\frac{\pi}{2}}) = (\angle c + \angle d) - \angle a - \angle b = (\pi) - (arctan^{-1}\left( \frac{1-\frac{1}{2\sqrt{2}}}{\frac{-1}{\sqrt{2}}} \right) + \pi) - (arctan^{-1}\left( \frac{1+\frac{1}{2\sqrt{2}}}{1-\frac{1}{\sqrt{2}}} \right) + \pi) = -0.7563 $
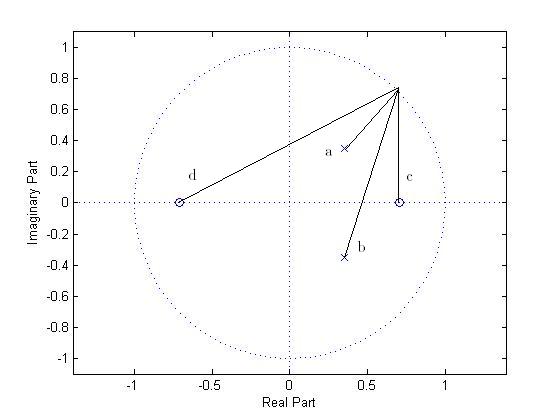
$ \omega =\frac{3\pi}{4} $
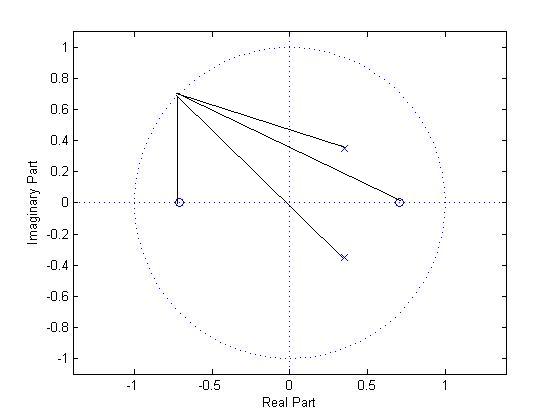
$ = \left| \frac{(\frac{-1}{\sqrt{2}} + j\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}})(\frac{-1}{\sqrt{2}} + j\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}})} { (\frac{-1}{\sqrt{2}} + j\frac{1}{\sqrt{2}}-(\frac{1}{\sqrt{2}} + j\frac{1}{\sqrt{2}}))(\frac{-1}{\sqrt{2}} + j\frac{1}{\sqrt{2}}-(\frac{1}{\sqrt{2}} - j\frac{1}{\sqrt{2}})) } \right| = \frac{2}{3} $
$ \angle H(e^{j\frac{3\pi}{4}}) = \angle c + \angle d - \angle a - \angle b = (arctan^{-1}\left( \frac{\frac{1}{\sqrt{2}}}{\frac{-2}{\sqrt{2}}} \right) + \pi) + \frac{\pi}{2} - (arctan^{-1}\left( \frac{\frac{1}{\sqrt{2}} - \frac{1}{2\sqrt{2}}}{\frac{1}{\sqrt{2}} - \frac{1}{2\sqrt{2}}} \right) + \pi) + \frac{3\pi}{4} = -0.9273 $
$ \omega =\pi $
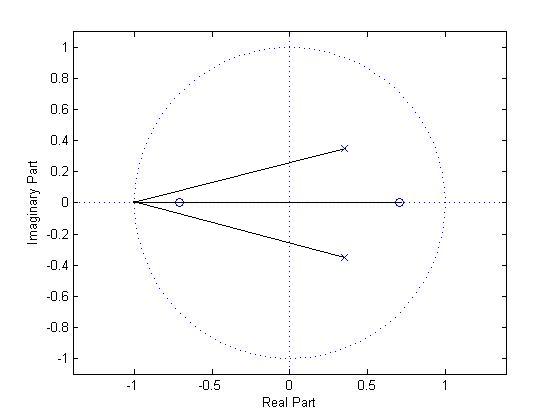
$ = \left| \frac{(-1+\frac{1}{\sqrt{2}})(-1-\frac{1}{\sqrt{2}})} { (-1-(\frac{1}{2\sqrt{2}} + j\frac{1}{2\sqrt{2}}))(-1-(\frac{1}{2\sqrt{2}} - j\frac{1}{2\sqrt{2}})) } \right| = 0.255 $
$ \angle H(e^{j\pi}) = (\angle c + \angle d) - \angle a - \angle b = 2\pi - 0 - 0 = 2\pi $
c. Is the system stable? Explain why or why not?
The system is causal and the ROC extends outwards from the outermost pole since |$ p_1 $| = |$ p_2 $| < 1 and this ROC contains the unit circle. Therefore the system is stable.
d. Find the difference equation for y[n] in terms of x[n], corresponding to this transfer function H(z).
$ H(z) = \frac{Y(z)}{X(z)} = \frac{1-\frac{1}{2}z^{-2}}{1-\frac{1}{\sqrt{2}} z^{-1} +\frac{1}{4} z^{-2}} $
$ Y(z)(1-\frac{1}{\sqrt{2}} z^{-1} +\frac{1}{4} z^{-2}) = X(z)(1-\frac{1}{2}z^{-2}) $
Taking inverse,
$ y[n]-\frac{1}{\sqrt{2}}y[n-1] + \frac{1}{4}y[n-2] = x[n] - \frac{1}{2}x[n-2] $
$ y[n] = x[n] - \frac{1}{2}x[n-2] +\frac{1}{\sqrt{2}}y[n-1] - \frac{1}{4}y[n-2] $
Q5.
$ y[n]=\frac{1}{8} \left( x[n]+x[n-1]+x[n-2]+x[n-3]+x[n-4]+x[n-5]+x[n-6]+x[n-7]\right) $
a.
$ h[n]=\frac{1}{8} \left( \delta[n]+\delta[n-1]+\delta[n-2]+\delta[n-3]+\delta[n-4]+\delta[n-5]+\delta[n-6]+\delta[n-7] \right) $
This is a finite duration response.
b.
$ H[z]=\frac{1}{8} \left( 1+z^{-1}+z^{-2}+z^{-3}+z^{-4}+z^{-5}+z^{-6}+z^{-7} \right) $
$ H[z]=\frac{1}{8} \left( \frac{1-z^{-8}}{1-z^{-1}} \right) $
c.
$ H[z]=\frac{1}{8} \left( \frac{z^{8}-1}{z^{7}(z-1)} \right) $
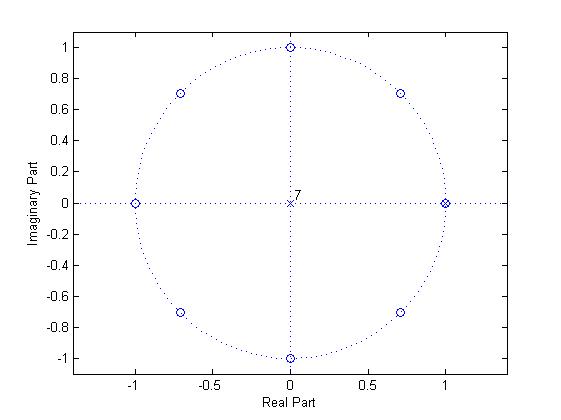
Poles:
$ p_1 = 1 $
$ p_2 = p_3 = ... = p_8 = 0 $
Zeros:
$ z^{8} - 1 = 0 $
$ z^{8} = e^{j2\pi } $
$ z = e^{j2\pi /8 } $
Generalizing,
$ z_k = e^{j2\pi k/8 } $ for k = 0,1,2,...,7
Q6.
a.
$ y[n]= \frac{1}{8} \left( x[n]-x[n-8]+y[n-1] \right) $
Using z-transform,
$ Y(z) = \frac{1}{8} \left( X(z)-X(z)e^{-j\omega 8} + Y(z)e^{-j\omega } \right) $
$ Y(z) (1 - e^{-j\omega }) = X(z) \frac{1}{8}(1 - e^{-j\omega 8}) $
$ H(z) = \frac{Y(z)}{X(z)} = \frac{1}{8} \left( \frac{ 1 - e^{-j\omega 8} } {1 - e^{-j\omega }} \right) $
b. Same as Q5, part c.
c.
H(z) can be re-written as
$ H[z]=\frac{1}{8} \left( 1+z^{-1}+z^{-2}+z^{-3}+z^{-4}+z^{-5}+z^{-6}+z^{-7} \right) $
Taking inverse Z-transform of H(z) -
$ h[n]=\frac{1}{8} \left( \delta[n]+\delta[n-1]+\delta[n-2]+\delta[n-3]+\delta[n-4]+\delta[n-5]+\delta[n-6]+\delta[n-7] \right) $
This is a finite duration response.
Back to HW7
Back to ECE 438 Fall 2010