| Line 22: | Line 22: | ||
[[Image:upsampling_process.jpg]] | [[Image:upsampling_process.jpg]] | ||
| − | The above figure is the general upsampling process by a factor of <math>L</math>, as | + | The above figure is the general upsampling process by a factor of <math>L</math>, as you did in Lab 4. |
The first upsampler inserting <math>L-1</math> zeros in between each sample. | The first upsampler inserting <math>L-1</math> zeros in between each sample. | ||
Revision as of 15:20, 19 September 2010
Solution to Q5 of Week 5 Quiz Pool
By Nyquist condition, the sampling frequency must be larger than the twice of maximum signal frequency, in order to avoid the aliasing when sampling.
$ \begin{align} x(t) &= \text{cos}(1000 \pi t) + \text{sin}(1500 \pi t) \\ &= \text{cos}(2\pi \times 500 t) + \text{sin}(2\pi \times 750 t) \end{align} \,\! $
Thus, it consists of two sinusoidal with frequencies equal to 500 Hz and 750 Hz, respectively.
Since the maximum frequency is 750 Hz, the sampling frequency must be greater than 1500 Hz, which is
$ F_s > 2\times 750 = 1500 \text{ Hz} \,\! $
Solution to Q6 of Week 5 Quiz Pool
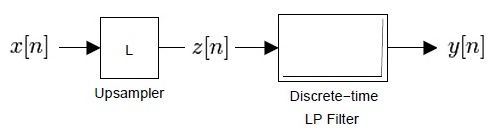
The above figure is the general upsampling process by a factor of $ L $, as you did in Lab 4.
The first upsampler inserting $ L-1 $ zeros in between each sample.
The frequency domain relationship betweeen a signal $ x[n] $ and its upsampled version $ z[n] $ can be shown to be the following,
$ Z(e^{jw}) = X(e^{jwL}) \,\! $
Therefore, the DTFT of $ z[n] $ is simply $ X(e^{jw}) $ compressed in frequency by a factor of $ L $.
Since $ X(e^{jw}) $ has a period of $ 2\pi $, $ Z(e^{jw}) $ will have a period of $ 2\pi/L $
All the original information of $ x[n] $ will be contained in the interval $ [-\pi/L,\;\pi/L] $ of $ Z(e^{jw}) $
Thus, the unwanted components in the intervals $ [-\pi,\;-\pi/L] $ and $ [\pi/L,\;\pi] $ needs to be filtered out.
Therefore, the cut-off frequency, $ f_c $ of the discrete-time low-pass filter (LPF) is $ f_c=\frac{\pi}{L} $, in general.
For the case of our question ($ L=2 $), the cut-off frequency is $ \frac{\pi}{2} $.
Back to Lab Week 5 Quiz Pool
Back to ECE 438 Fall 2010 Lab Wiki Page
Back to ECE 438 Fall 2010