| Line 3: | Line 3: | ||
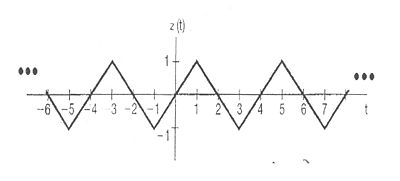
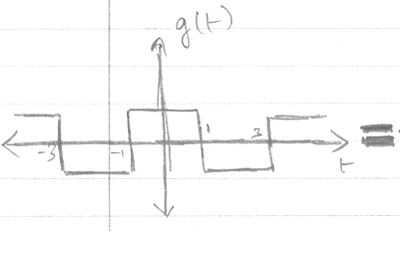
Let <math> g(t) = \left ( \frac{dz}{dt} \right ) </math> | Let <math> g(t) = \left ( \frac{dz}{dt} \right ) </math> | ||
| − | [[Image:7b1_OldKiwi.jpg]] | + | [[Image:7b1_OldKiwi.jpg|400px|]] |
| − | [[Image:7b2_OldKiwi.jpg]] | + | [[Image:7b2_OldKiwi.jpg|400px|]] |
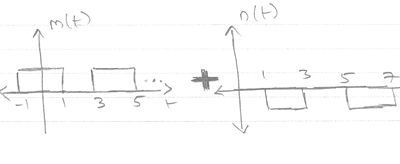
Therefore, <math> m_k = \left ( \frac {1}{k\pi} \sin ( \frac {k\pi}{2} ) \right) , n_k = \left( \frac {-1}{k\pi} \sin ( \frac {k\pi}{2} ) e^\frac{-j2k\pi2}{4} \right)</math> | Therefore, <math> m_k = \left ( \frac {1}{k\pi} \sin ( \frac {k\pi}{2} ) \right) , n_k = \left( \frac {-1}{k\pi} \sin ( \frac {k\pi}{2} ) e^\frac{-j2k\pi2}{4} \right)</math> | ||
Revision as of 11:19, 1 July 2008
Let $ g(t) = \left ( \frac{dz}{dt} \right ) $
Therefore, $ m_k = \left ( \frac {1}{k\pi} \sin ( \frac {k\pi}{2} ) \right) , n_k = \left( \frac {-1}{k\pi} \sin ( \frac {k\pi}{2} ) e^\frac{-j2k\pi2}{4} \right) $