(New page: When applying K-nearest neighbor (KNN) method or Artifical Neural Network (ANN) method for classification, the first question we need to answer is how to choose the model (i.e. in KNN what...) |
|||
| Line 17: | Line 17: | ||
4. Do with all <math>\lambda</math> and choose one that gives us the smallest overall estimated error. | 4. Do with all <math>\lambda</math> and choose one that gives us the smallest overall estimated error. | ||
| + | |||
| + | |||
| + | [[Image:fig_Old Kiwi.jpg]] | ||
| + | |||
| + | |||
| + | '''Figure 1: ''the way to split the data set in this technique''''' | ||
Latest revision as of 13:04, 17 April 2008
When applying K-nearest neighbor (KNN) method or Artifical Neural Network (ANN) method for classification, the first question we need to answer is how to choose the model (i.e. in KNN what K should be, or in ANN, how many hidden layers we need?).
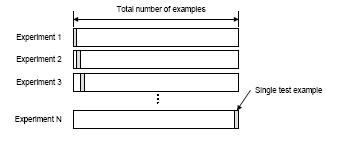
A popularly used method is the leave-one-out cross validation. Let's assume we want to find the optimum parameter lamda among M choices. (in KNN case, $ \lambda $ is the K, in ANN, $ \lambda $ is the number of the hidden layer). Assume that we have a data set of N samples.
For each choice of lamda, do the following steps:
1. Do N experiements. In each experiement, use N-1 samples for training, and leav only 1 sample for testing.
2. Compute the testing error $ E_i $, $ i=1,..,N $
3. After N experiments, compute the overall estimated error:
$ E_\lambda = \frac{1}{N}\left( {\sum\limits_{i = 1}^N {E_i } } \right) $
4. Do with all $ \lambda $ and choose one that gives us the smallest overall estimated error.
Figure 1: the way to split the data set in this technique