Difference between revisions of "Linear Discriminant Functions Old Kiwi" - Rhea

Revision as of 11:03, 17 March 2008

From Duda, Hart & Stock Textbook chapter 5.2

Discriminant fuction that is a linear combination of the component x
$ g(x)=w^Tx +w_o $

$ w=[w1, w2, w3,...,wd] $ => weight vector
$ w_o $ =>bias or threshold weight

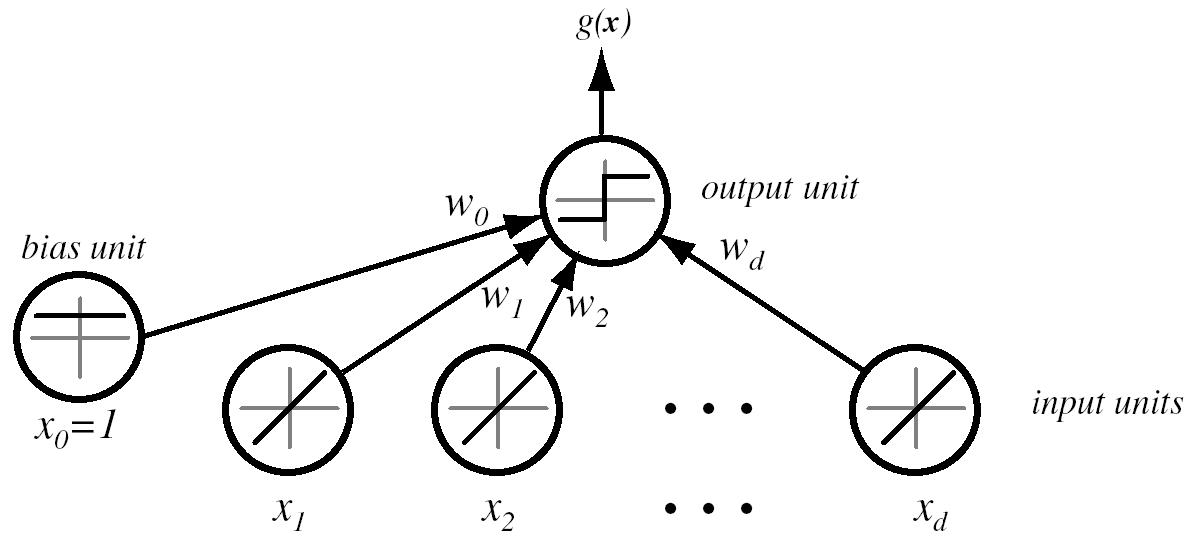
Two-catergory case
Decide w1 if $ g(x)>0 =>w^Tx > -wo $
Decide w2 if $ g(x) <0 =>w^Tx < -wo $
If $ g(x)=0 $ then it can we assigned to any class or be left undefined

$ g(x)=0 $ define a decision surface (which is a hyperplane) that separates w1 and w2 points

The hyperplane divides the feature space into two halfs: region R1 for w1 and region R2 for w2
w is normal to any vector laying in the hyperplane

The distance from x to the hyperplane is $ g(x)/||w|| $
The distance from the origin to the hyperplane is $ w_o/||w|| $

Proof:
$ x=xp+r(w/||w||) $

• xp = normal projectionof x onto hyperplane(H)
  
• r = desired algebraic distance - positive if on the positive side and negative if on the negative side
  

Because $ g(xp) =0 $
$ g(x) =w^Tx + wo =r||w|| $
therefore $ r = g(x)/||w|| $

[Image:decision_bound.jpg]]

Multicategory case

Some ways to devise multicategory classifiers
-reduce the problem to c-1 two-class problems; where teh ith problem is solvd by a linear discriminant function that separates points assigned to w_i from those not assigned to w_i
-use c(c-1)/2 linear discriminants; one for every pair of classes
-defining c linear discriminant functions $ g_i(x)=w^Tx_i+w_{i_o} $ $ i=1,..,c $
assigning x to w_i if $ g_i(x)>g_j(x) {\forall} j !=i $

A linear machine divides the feature space into c decision regions

If Region i and region j are contiguous, the boundary between them is a portion of the hyperplane Hij defined by $ g_i(x)=g_j(x) $ => $ (w_i-w_j)^Tx+(w_{i_o}-w_{j_o})=0 $

$ w_i-w_j $ is normal to Hij
$ (g_i-g_j)/||w_i-w_j|| $ is the distance from x to Hij

References

Duda, Hart, and Stork, Chapter 5, section 5.2