(→The complex plane) |
|||
| Line 3: | Line 3: | ||
== The complex plane == | == The complex plane == | ||
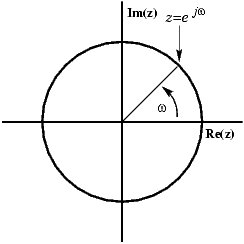
| + | In order to get further insight into the relationship between the Fourier Transform and the Z-Transform it is useful to look at the complex plane or z-plane. Take a look at the complex plane: | ||
| + | [[Image:zplane1_ECE301Fall2008mboutin.jpg]] | ||
Revision as of 16:15, 3 December 2008
Basic definition of the Z-Transform
The Z-transform of a sequence is defined as $ H(z) = \sum^{\infty}_{n = -\infty} h[n]z^{-n} $
The complex plane
In order to get further insight into the relationship between the Fourier Transform and the Z-Transform it is useful to look at the complex plane or z-plane. Take a look at the complex plane: