| Line 1: | Line 1: | ||
| − | == Guess the Periodic Signal | + | == Guess the Periodic Signal == |
Suppose a DT singal satisfies the following properties: | Suppose a DT singal satisfies the following properties: | ||
| Line 47: | Line 47: | ||
| − | Therefore, the signal | + | Therefore, the signal described by the five properties is |
<math>\,x[n]=1-\frac{1}{2}e^{j\frac{\pi}{2}n}-\frac{1}{2}e^{j\frac{3\pi}{2}n}\,</math> | <math>\,x[n]=1-\frac{1}{2}e^{j\frac{\pi}{2}n}-\frac{1}{2}e^{j\frac{3\pi}{2}n}\,</math> | ||
| + | |||
| + | |||
| + | [[Image:Jkubasci guess signal_ECE301Fall2008mboutin.png]] | ||
Latest revision as of 19:40, 25 September 2008
Guess the Periodic Signal
Suppose a DT singal satisfies the following properties:
1. x[n] is periodic with period 4 and has Fourier coefficients $ \,a_k\, $.
2. $ \,\sum_{n=0}^{3}x[n]=4\, $
3. The Fourier coefficients $ \,a_1\, $ and $ \,a_3\, $ are equal.
4. $ \,a_1\, $ is the maximal negative value while $ \,a_2\, $ is non-positive.
5. The value of the signal at $ \,n=0\, $ is zero.
Answer
The first property tells us that the signal is in the form of
$ \,x[n]=\sum_{k=0}^{3}a_ke^{jk\frac{2\pi}{4}n}\, $
$ \,x[n]=a_0 + a_1e^{j\frac{\pi}{2}n} + a_2e^{j\pi n} + a_3e^{j\frac{3\pi}{2}n}\, $
The second property can be used to calculate the average of the signal over one period, which is precisely what $ \,a_0\, $ is
$ \,a_0=\frac{4}{T}=1\, $
The last three properties can be combined to figure out $ \,a_1, a_2, a_3\, $. The fifth property shows that
$ \,x[0]=0\, $
$ \,0=a_0 + a_1e^{0} + a_2e^{0} + a_3e^{0}\, $
$ \,0=1 + a_1 + a_2 + a_3\, $
By the third property, we can rewrite this as
$ \,-1=2a_1+a_2\, $
Property four is satisfied when $ \,a_2=0\, $
$ \,-1=2a_1\, $
$ \,a_1=a_3=-\frac{1}{2}\, $
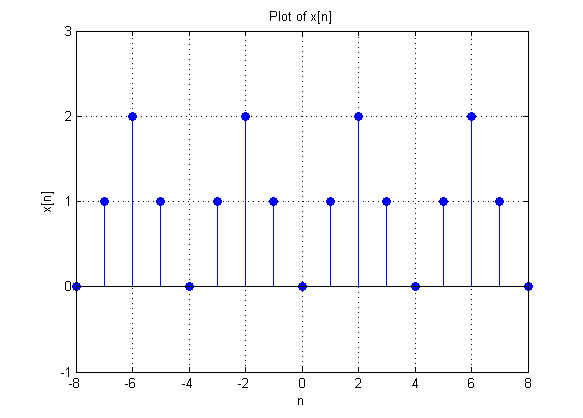
Therefore, the signal described by the five properties is
$ \,x[n]=1-\frac{1}{2}e^{j\frac{\pi}{2}n}-\frac{1}{2}e^{j\frac{3\pi}{2}n}\, $