| Line 1: | Line 1: | ||
I choose y(t)=cos(t) as my continous signal. | I choose y(t)=cos(t) as my continous signal. | ||
There is no doubt that y(t)=cos(t) is periodic because cos(t + T) = cos(t) where its fundamental period is 2*π | There is no doubt that y(t)=cos(t) is periodic because cos(t + T) = cos(t) where its fundamental period is 2*π | ||
| − | |||
| + | ---- | ||
| + | == Periodic Function == | ||
| + | |||
| + | |||
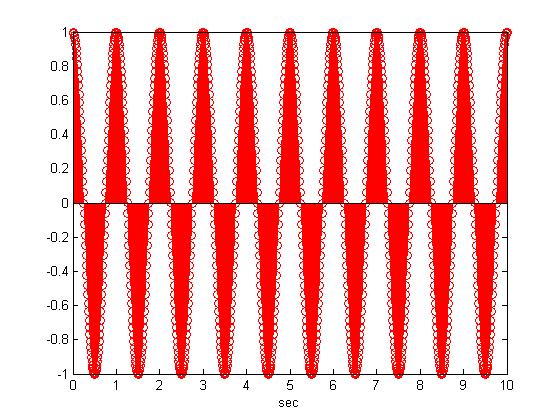
| + | First I sample the signal y(t)=cos(t) at 100 Hz and so we get the following discrete signal which is periodic | ||
| − | |||
[[Image:periodic_goklani_ECE301Fall2008mboutin.jpg]] | [[Image:periodic_goklani_ECE301Fall2008mboutin.jpg]] | ||
| + | |||
| + | |||
| + | ---- | ||
| + | |||
| + | == Non periodic funtion == | ||
| + | |||
| + | |||
| + | |||
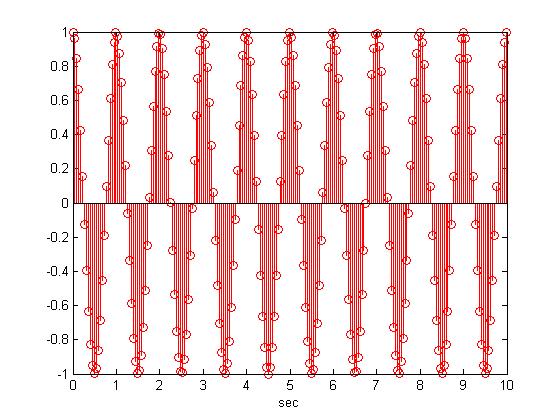
| + | * Now if I sample the signal y(t)=cos(t) at 22.22 Hz then we get the following discrete signal which is not periodic | ||
| + | |||
| + | |||
| + | |||
| + | [[Image:non periodic_goklani_ECE301Fall2008mboutin.jpg]] | ||
| + | |||
| + | |||
| + | ---- | ||
| + | |||
| + | == Recurring non periodic function = periodic == | ||
| + | |||
| + | Now let us shift the non periodic function y(t)= <math>{e^{3t}}</math> | ||
| + | |||
| + | |||
| + | we use the following matlab code | ||
| + | %referred the code of paul sceffler | ||
| + | <pre> | ||
| + | clc | ||
| + | clear | ||
| + | |||
| + | t=0.01:.01:1; | ||
| + | x=exp(3*t); | ||
| + | i=[]; | ||
| + | for d=1:10 | ||
| + | i=[i,x]; | ||
| + | end | ||
| + | |||
| + | t=[0.01:.01:10]; | ||
| + | plot(t,i) | ||
| + | </pre> | ||
| + | |||
| + | |||
| + | |||
| + | ---- | ||
| + | [[Image:recurring non periodic_goklani_ECE301Fall2008mboutin.jpg]] | ||
| + | |||
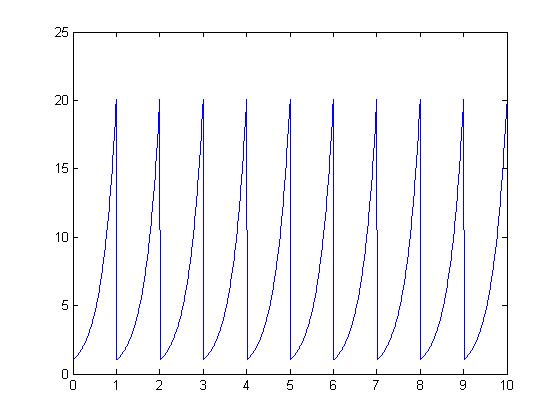
| + | we see above that the non-periodic signal is now periodic | ||
Revision as of 20:41, 11 September 2008
I choose y(t)=cos(t) as my continous signal. There is no doubt that y(t)=cos(t) is periodic because cos(t + T) = cos(t) where its fundamental period is 2*π
Periodic Function
First I sample the signal y(t)=cos(t) at 100 Hz and so we get the following discrete signal which is periodic
Non periodic funtion
- Now if I sample the signal y(t)=cos(t) at 22.22 Hz then we get the following discrete signal which is not periodic
Recurring non periodic function = periodic
Now let us shift the non periodic function y(t)= $ {e^{3t}} $
we use the following matlab code
%referred the code of paul sceffler
clc
clear
t=0.01:.01:1;
x=exp(3*t);
i=[];
for d=1:10
i=[i,x];
end
t=[0.01:.01:10];
plot(t,i)
we see above that the non-periodic signal is now periodic