(→Periodic Signals Revisited) |
(→Periodic Signals Revisited) |
||
| Line 17: | Line 17: | ||
<br> | <br> | ||
<br> | <br> | ||
| + | == == | ||
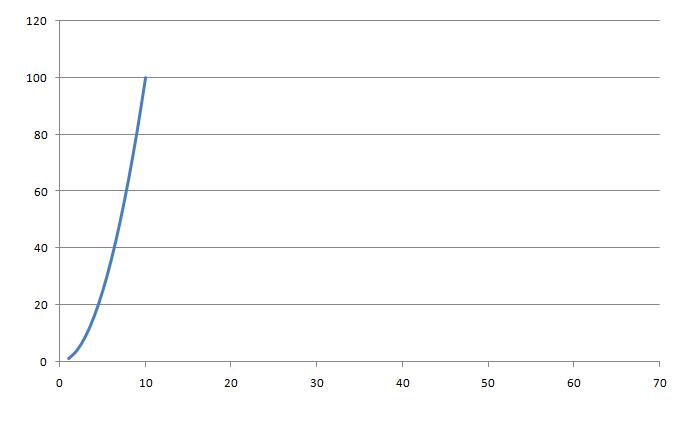
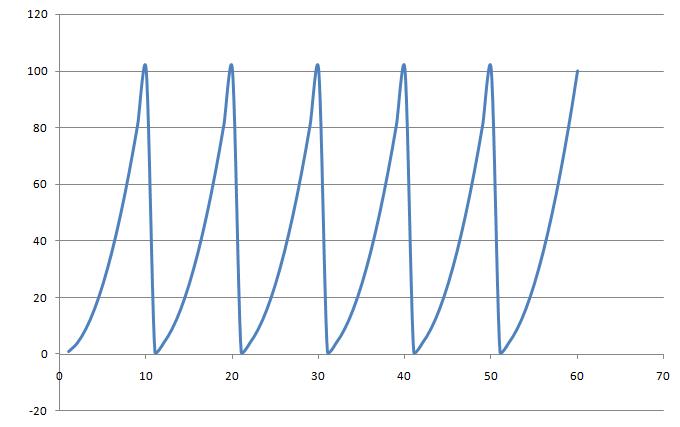
2. By adding up several 10 unit cycles of the function <math>y(x)=x^2\!</math> we can turn a non-periodic signal into a periodic signal: | 2. By adding up several 10 unit cycles of the function <math>y(x)=x^2\!</math> we can turn a non-periodic signal into a periodic signal: | ||
[[Image:Xsquare_ECE301Fall2008mboutin.jpg]] | [[Image:Xsquare_ECE301Fall2008mboutin.jpg]] | ||
[[Image:Xsquare2_ECE301Fall2008mboutin.jpg]] | [[Image:Xsquare2_ECE301Fall2008mboutin.jpg]] | ||
Revision as of 18:29, 11 September 2008
Periodic Signals Revisited
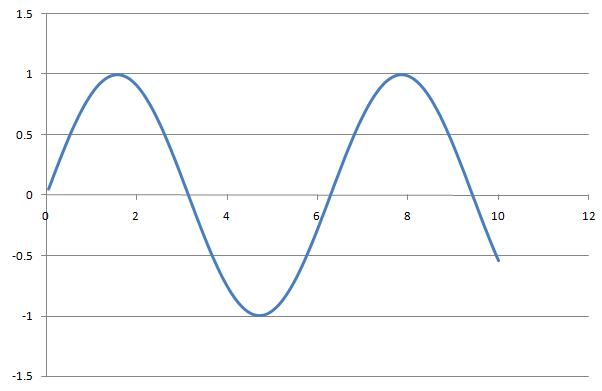
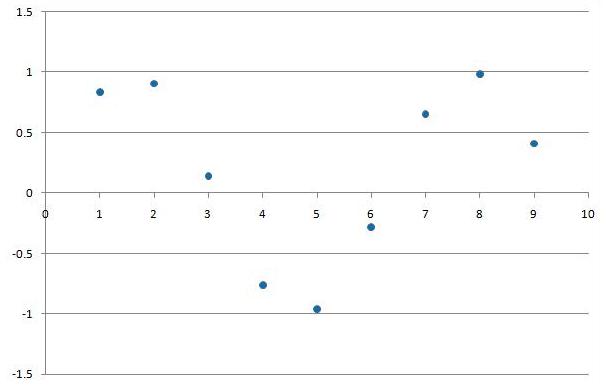
1. By sampling at different frequencies the signal $ y=sin(x)\! $ can appear as both periodic and non-periodic in DT. For example:
$ y[n]=sin[n] \! $ with a sample rate of 1
$ y[n]=sin[n] \! $ with a sample rate of $ pi/4 \! $
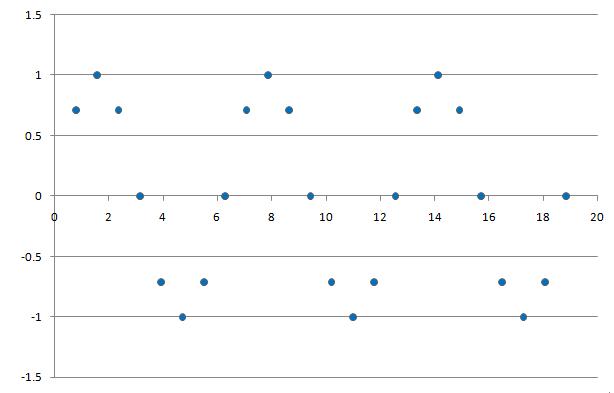
The second graph has no integer value of N where y[n]=y[n+N], thus it is non-periodic.
The third graph clearly shows there is an integer value of N where y[n]=y[n+N], thus it is periodic.
2. By adding up several 10 unit cycles of the function $ y(x)=x^2\! $ we can turn a non-periodic signal into a periodic signal: