| Line 21: | Line 21: | ||
== Example of a System that is not Time Invariant == | == Example of a System that is not Time Invariant == | ||
| − | Let <math>y(t)=2tx(t)\!</math>. | + | Let <math>y(t)=2tx(t)\!</math>. Because the two outputs are not equal, the system is not time invariant. Rather, it is called time variant. |
<br> | <br> | ||
<br> | <br> | ||
Proof: | Proof: | ||
<br> | <br> | ||
| − | [[Image: | + | [[Image:Timvar_ECE301Fall2008mboutin.jpg]] |
Revision as of 15:16, 11 September 2008
Time Invariance
A system is time-invariant if for any input $ x(t)\! $ and any $ t_0\! $ (where $ t_0\! $ is a real number) the response to the shifted input $ x(t-t_0)\! $ is $ y(t-t_0)\! $.
One can show a system is time invarient by proving
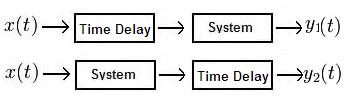
where $ y_1(t)\! $ and $ y_2(t)\! $ are equal.
Example of a Time Invariant System
Let $ y(t)=2x(t)\! $. The system is time invarient if for input $ x(t-t_0)\! $ the response is $ 2x(t-t_0)\! $.
Proof:

Example of a System that is not Time Invariant
Let $ y(t)=2tx(t)\! $. Because the two outputs are not equal, the system is not time invariant. Rather, it is called time variant.
Proof:


