(→Non-Linear System) |
(→Non-Linear System) |
||
| Line 29: | Line 29: | ||
[[Image:System3_ECE301Fall2008mboutin.jpg]] | [[Image:System3_ECE301Fall2008mboutin.jpg]] | ||
| + | |||
| + | [[Image:System4_ECE301Fall2008mboutin.jpg]] | ||
Revision as of 14:42, 11 September 2008
Linearity
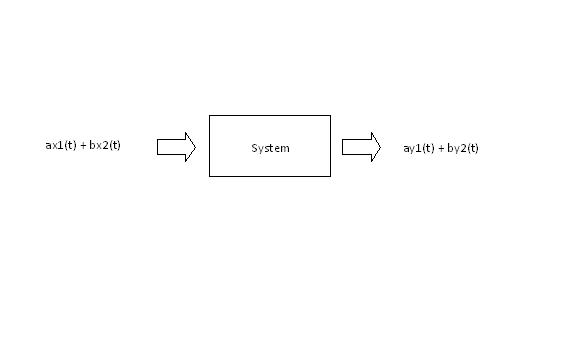
In my own words, a linear system is a system in which superposition applies. For example, if two inputs x1(t) and x2(t) are applied to the system, the output of the system will the sum of the responses to both inputs, y(t) = y1(t) + y2(t).
For example,
x1(t) + x2(t) $ \rightarrow $ system $ \rightarrow $ y(t) = y1(t) + y2(t)
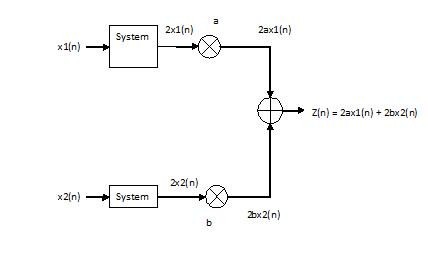
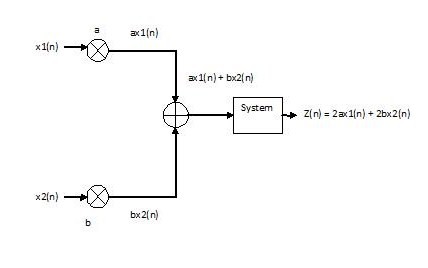
Linear System
x[n] $ \rightarrow $ system $ \rightarrow $ y[n] = 2x[n]
Proof:
Based on Prof Mimi's definition 3 of Linearity, since the system produces the same output for both cases, the system is linear.
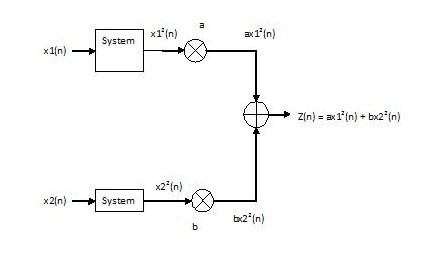
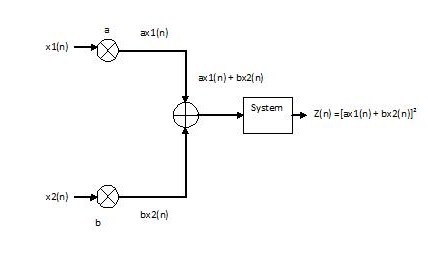
Non-Linear System
x[n] $ \rightarrow $ system $ \rightarrow $ $ y[n] = x[n]^2 $
Proof: