(→Linear System) |
|||
| Line 2: | Line 2: | ||
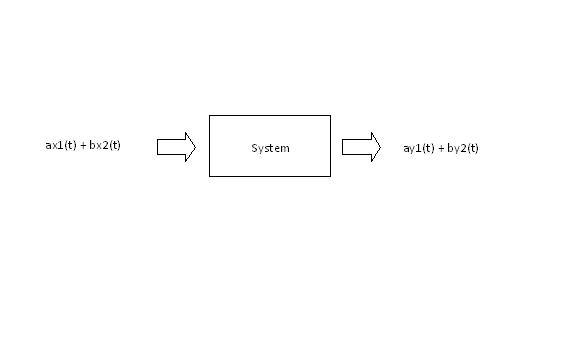
In my own words, a linear system is a system in which superposition applies. For example, if two inputs x1(t) and x2(t) are applied to the system, the output of the system will the sum of the responses to both inputs, y(t) = y1(t) + y2(t). | In my own words, a linear system is a system in which superposition applies. For example, if two inputs x1(t) and x2(t) are applied to the system, the output of the system will the sum of the responses to both inputs, y(t) = y1(t) + y2(t). | ||
| + | |||
| + | For example, | ||
| + | |||
| + | x1(t) + x2(t) <math>\rightarrow</math> system <math>\rightarrow</math> y(t) = y1(t) + y2(t) | ||
| + | |||
[[Image: System_ECE301Fall2008mboutin.JPG]] | [[Image: System_ECE301Fall2008mboutin.JPG]] | ||
| Line 7: | Line 12: | ||
x[n] <math>\rightarrow</math> system <math>\rightarrow</math> y[n] = 2x[n] | x[n] <math>\rightarrow</math> system <math>\rightarrow</math> y[n] = 2x[n] | ||
| + | |||
| + | Proof: | ||
| + | |||
| + | |||
==Non-Linear System== | ==Non-Linear System== | ||
| + | |||
| + | x[n] <math>\rightarrow</math> system <math>\rightarrow</math> <math>y[n] = x[n]^3</math> | ||
Revision as of 09:58, 11 September 2008
Linearity
In my own words, a linear system is a system in which superposition applies. For example, if two inputs x1(t) and x2(t) are applied to the system, the output of the system will the sum of the responses to both inputs, y(t) = y1(t) + y2(t).
For example,
x1(t) + x2(t) $ \rightarrow $ system $ \rightarrow $ y(t) = y1(t) + y2(t)
Linear System
x[n] $ \rightarrow $ system $ \rightarrow $ y[n] = 2x[n]
Proof:
Non-Linear System
x[n] $ \rightarrow $ system $ \rightarrow $ $ y[n] = x[n]^3 $