Difference between revisions of "HW2.A Jeff Kubascik ECE301Fall2008mboutin" - Rhea

Revision as of 16:08, 11 September 2008

Part 1

The function was chosen at random from HW1: HW1.4 Hang Zhang - Periodic vs Non-period Functions_ECE301Fall2008mboutin

$ \,x(t)=2cos(2\pi t)\, $

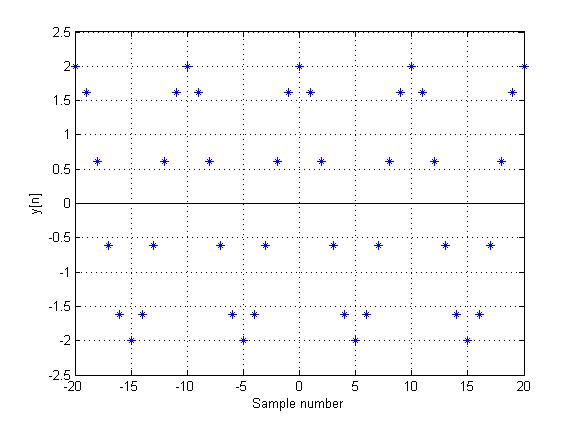
Periodic Signal in DT:

If $ x(t) $ is sampled at $ period=0.1 $, the function

$ \,y[n]=x[0.1n]=2cos(\frac{2\pi n}{10})\, $

is periodic, since

$ \,\exists N\in \mathbb{Z}, N\not= 0\, $ such that $ \,y[n]=y[n+N], \forall n\in \mathbb{Z}\, $

$ \,2cos(\frac{2\pi n}{10})=2cos(\frac{2\pi n}{10}+\frac{2\pi N}{10})\, $

This is true when

$ \,\frac{2\pi N}{10}=2\pi \, $

$ \,N=10\, $

This can be seen in the following plot:

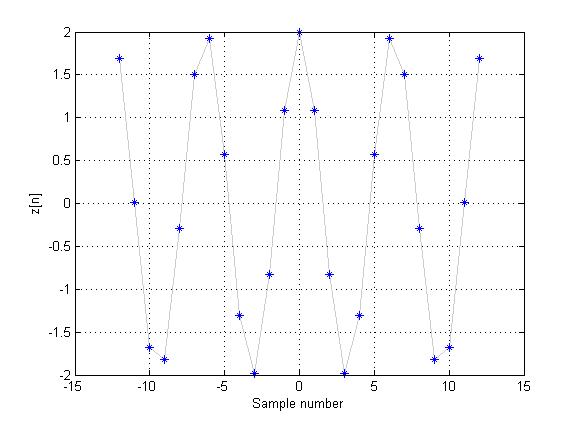
Non-Periodic Signal in DT:

However, if $ x(t) $ is sampled at $ period=1/2\pi $, the function

$ \,z[n]=x[\frac{n}{2\pi}]=2cos(n)\, $

is not periodic in DT, since there is no integer $ N\in \mathbb{Z}, N\not= 0 $ such that

$ \,z[n]=z[n+N], \forall n\in \mathbb{Z}\, $

$ \,2cos(n)=2cos(n+N)\, $

This would be true when

$ \,N=2\pi k, k\in \mathbb{Z}, k\not= 0\, $

$ \,\frac{N}{k}=2\pi \, $

but, $ 2\pi $ is irrational, thus there are no values for the integers $ \,N,k\, $ that will satisfy this equation.

This can be seen in the following plot:

Part 2

TODO: Having problems performing this on arbitrary functions, such as $ \,x(t)=e^{t}\, $, since the infinite sum will result with an undefined function.