(→Part 1) |
(→Part 1) |
||
| Line 26: | Line 26: | ||
<math>\,z[n]=x[\frac{n}{2\pi}]=2cos(n)\,</math> | <math>\,z[n]=x[\frac{n}{2\pi}]=2cos(n)\,</math> | ||
| − | Is not periodic in DT, since | + | Is not periodic in DT, since is no real number <math>k</math> such that |
| + | |||
| + | <math>\,z[n]=z[n+kN], \forall N\in Z\,</math> | ||
| + | |||
This can be seen in the following plot (notice how the values do not line up horizontally): | This can be seen in the following plot (notice how the values do not line up horizontally): | ||
Revision as of 12:28, 11 September 2008
Part 1
The function was chosen at random from HW1: HW1.4 Hang Zhang - Periodic vs Non-period Functions_ECE301Fall2008mboutin
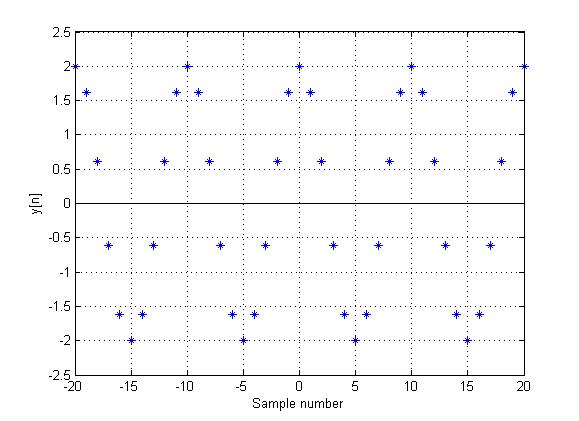
$ \,x(t)=2cos(2\pi t)\, $
Periodic Signal in DT:
If $ x(t) $ is sampled at $ period=0.1 $, the function
$ \,y[n]=x[0.1n]=2cos(\frac{2\pi n}{10})\, $
would be periodic, since
$ \,y[n]=y[n+10N], \forall N\in Z\, $
This can be seen in the following plot (notice how the values lines up horizontally):
Non-Periodic Signal in DT:
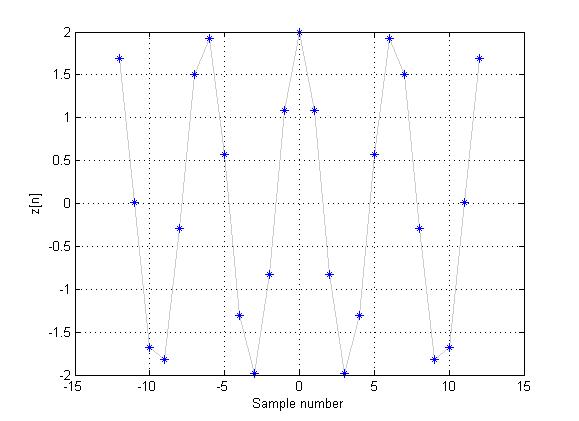
However, if $ x(t) $ is sampled at $ period=1/2\pi $, the function
$ \,z[n]=x[\frac{n}{2\pi}]=2cos(n)\, $
Is not periodic in DT, since is no real number $ k $ such that
$ \,z[n]=z[n+kN], \forall N\in Z\, $
This can be seen in the following plot (notice how the values do not line up horizontally):