(→Periodic Signals from Non-periodic signals) |
|||
| (3 intermediate revisions by the same user not shown) | |||
| Line 29: | Line 29: | ||
t = [0.001:0.001:12]; | t = [0.001:0.001:12]; | ||
plot(t,z); | plot(t,z); | ||
| − | < | + | </pre> |
I have created a signal with a period of 4units. | I have created a signal with a period of 4units. | ||
| + | |||
[[Image:two_ECE301Fall2008mboutin.jpg]] | [[Image:two_ECE301Fall2008mboutin.jpg]] | ||
| + | |||
Note: I have referred to Wei Jian Chan's matlab program to help me get started. I hope you do not mind. | Note: I have referred to Wei Jian Chan's matlab program to help me get started. I hope you do not mind. | ||
Latest revision as of 08:36, 11 September 2008
We know that x(t)=cos(t) is a periodic CT signal because it follows the rule, x(t+T)=x(t). It is periodic with a period T=$ \barwedge $
Now by sampling the CT signal at the right frequencies will yield a periodic DT signal. It is noticed that the signal is a DT periodic signal when it is sampled at rate $ 2*pi $,$ pi $.
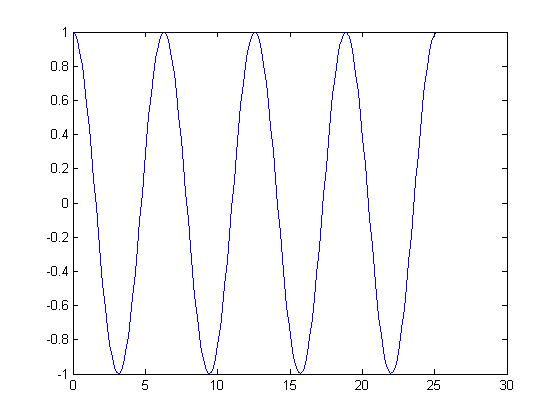
When you have a signal at a sampling rate of $ 2*pi $ we get a periodic DT signal.
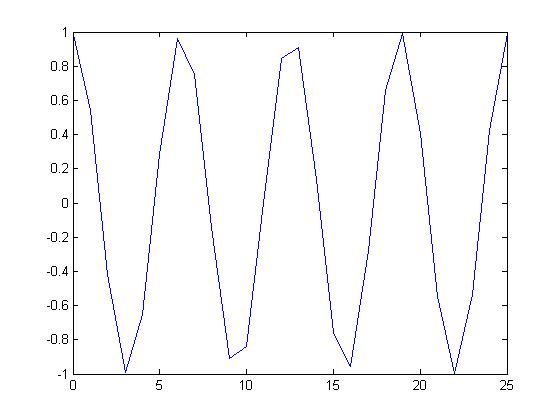
Now by sampling the CT signal at a random sampling rate of 1 we get a non periodic DT signal.
Periodic Signals from Non-periodic signals
We are told that we can create a periodic signal by adding together an infinite number of shifted copies of non-periodic signals periodically.
Now let me consider a non periodic signal y=x. Now this can be made periodic by shifting it by a period of t0 and adding the sum of the shifted copies.
i.e
$ \sum_{-infty}^\infty\ {x(t-nt0)} $
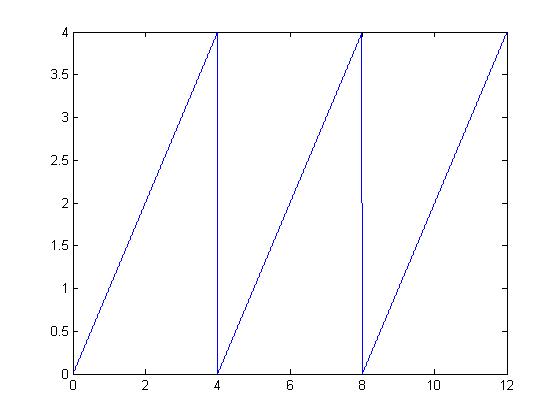
Now the matlab code to achieve this would be,
t0 = [0.001:0.001:4]; t0_1 = [4.001:0.001:8]; t0_2 = [8.001:0.001:12]; y_a = t0; y_b = t0_1 - 4; y_c = t0_2 - 8; z = [y_a y_b y_c]; t = [0.001:0.001:12]; plot(t,z);
I have created a signal with a period of 4units.
Note: I have referred to Wei Jian Chan's matlab program to help me get started. I hope you do not mind.