(→Part B) |
(→Part A) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
== Part A == | == Part A == | ||
| + | The periodic signal I used in Part A was <math>y=sin(x)</math>. | ||
| + | |||
| + | To create a DT signal from the above periodic CT signal I first sampled at an integer frequency of 1. The result was a non-periodic function.<br> | ||
| + | [[Image:Sinindt-rfscotthw2_ECE301Fall2008mboutin.jpg|frame|none|This plot was the result of sampling the CT signal with frequency 1. The squares are the sampled points.]] | ||
| + | <br> | ||
| + | It is easily seen that when sampled at this frequency the resulting DT signal is non-periodic. | ||
| + | <br> | ||
| + | To create a periodic DT signal of this function, I then sampled the original CT signal at <math>\pi \over 8</math>. | ||
| + | <br> | ||
| + | [[Image:Periodicindt-rfscotthw2_ECE301Fall2008mboutin.jpg|frame|none|This plot was the result of sampling the CT signal with frequency <math>\pi \over 8</math>. The sampled data points are represented by squares on the plot.]] | ||
| + | <br> | ||
| + | When the original CT signal is sampled at <math>\pi \over 8</math> it is now a periodic DT function. | ||
== Part B == | == Part B == | ||
| Line 15: | Line 27: | ||
plot(t,y) | plot(t,y) | ||
</pre> | </pre> | ||
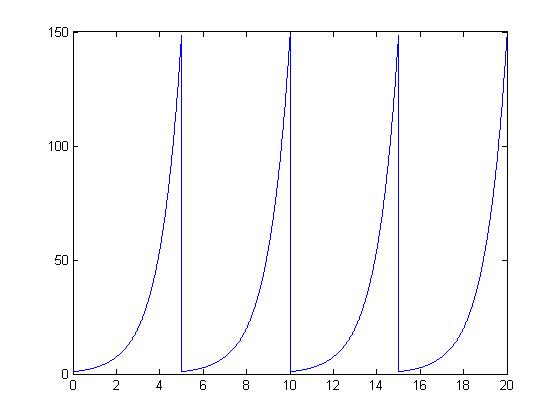
| − | What this does is repeats the function with a period of 5, and creates 4 full periods. | + | What this does is repeats the function with a period of 5, and creates 4 full periods.<br> |
[[Image:Hw2b-rfscott_ECE301Fall2008mboutin.jpg]] | [[Image:Hw2b-rfscott_ECE301Fall2008mboutin.jpg]] | ||
Latest revision as of 05:22, 11 September 2008
Part A
The periodic signal I used in Part A was $ y=sin(x) $.
To create a DT signal from the above periodic CT signal I first sampled at an integer frequency of 1. The result was a non-periodic function.
It is easily seen that when sampled at this frequency the resulting DT signal is non-periodic.
To create a periodic DT signal of this function, I then sampled the original CT signal at $ \pi \over 8 $.
When the original CT signal is sampled at $ \pi \over 8 $ it is now a periodic DT function.
Part B
The signal I used to transform into a periodic function was $ y=e^x $.
I did this in MATLAB using the following code:
t = [.01:.01:5]; func = exp(t); y = []; for lcv=1:4 y = [y,func]; end t = [.01:.01:20]; plot(t,y)
What this does is repeats the function with a period of 5, and creates 4 full periods.