| (9 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | ==Definition== | ||
The easiest way to think of time invariance is to use the vertical and horizontal line test. x(t) is the horizontal axis and y(t) is the vertical axis. | The easiest way to think of time invariance is to use the vertical and horizontal line test. x(t) is the horizontal axis and y(t) is the vertical axis. | ||
x(t) --> system 1 --> y(t) | x(t) --> system 1 --> y(t) | ||
| − | + | [[Image:vertical_ECE301Fall2008mboutin.jpg]] | |
| + | |||
| + | [[Image:horizontal_ECE301Fall2008mboutin.jpg]] | ||
| + | |||
| + | ==Time Invariant System== | ||
| + | <math>y=exp(x)</math> | ||
| + | This function passes both the horizontal and vertical line tests. | ||
| + | [[Image:TI_ECE301Fall2008mboutin.jpg]] | ||
| + | |||
| + | ==Non-Time Invariant System== | ||
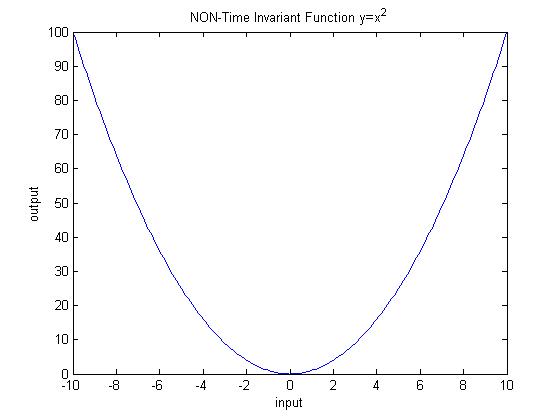
| + | <math>y=x^2</math> | ||
| + | This function fails the horizontal line test. | ||
| + | [[Image:NonTI_ECE301Fall2008mboutin.jpg]] | ||
Latest revision as of 13:25, 10 September 2008
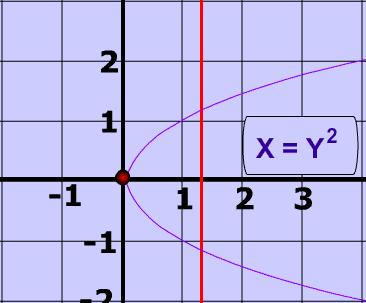
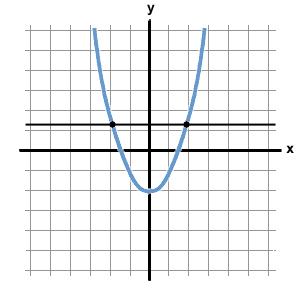
Definition
The easiest way to think of time invariance is to use the vertical and horizontal line test. x(t) is the horizontal axis and y(t) is the vertical axis.
x(t) --> system 1 --> y(t)
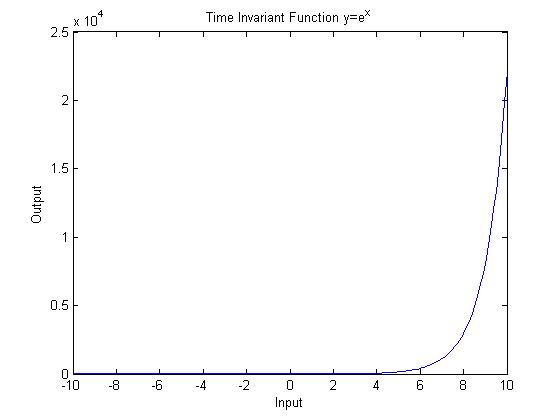
Time Invariant System
$ y=exp(x) $
This function passes both the horizontal and vertical line tests.
Non-Time Invariant System
$ y=x^2 $
This function fails the horizontal line test.
