| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | Consider the function <math> | + | Consider the function <math>f(t) = e^{2\pi j}</math> |
| − | + | In order to determine if the function is periodic or not we need to use the formula: | |
| + | |||
| + | <math>\omega0/(2\pi) = k/N</math> | ||
| + | |||
| + | where in this case the function is periodic because <math>\omega0 = 2\pi</math> so k and N can be any number such that k = N and k/N is the rational number 1. | ||
| + | |||
| + | For the function to be non-periodic, if <math>\omega0 = \sqrt{2}\pi</math> then the function would be non-periodic because k/N would be equal to a irrational number. | ||
| + | |||
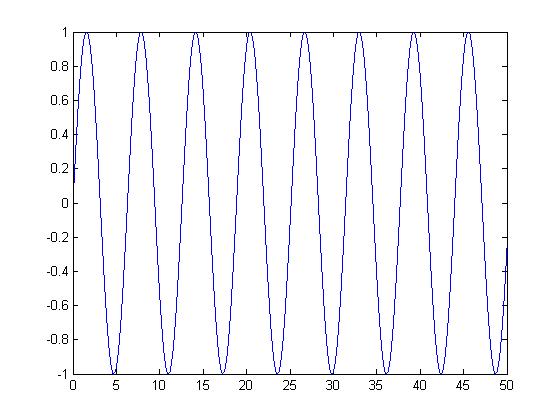
| + | The Periodic Signal is shown below: | ||
| + | |||
| + | [[Image:figure1_ECE301Fall2008mboutin.jpg]] | ||
| + | |||
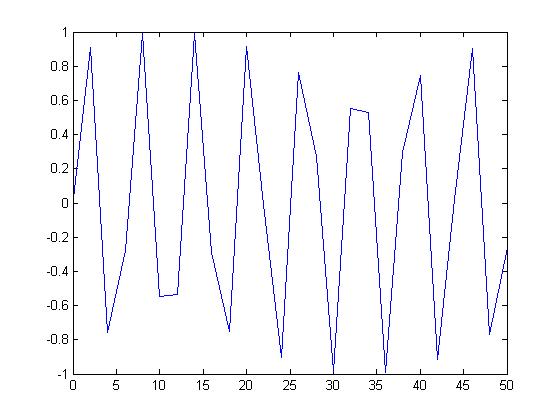
| + | And here is the non-periodic signal: | ||
| + | |||
| + | [[Image:figure2_ECE301Fall2008mboutin.jpg]] | ||
Latest revision as of 13:16, 12 September 2008
Consider the function $ f(t) = e^{2\pi j} $
In order to determine if the function is periodic or not we need to use the formula:
$ \omega0/(2\pi) = k/N $
where in this case the function is periodic because $ \omega0 = 2\pi $ so k and N can be any number such that k = N and k/N is the rational number 1.
For the function to be non-periodic, if $ \omega0 = \sqrt{2}\pi $ then the function would be non-periodic because k/N would be equal to a irrational number.
The Periodic Signal is shown below:
And here is the non-periodic signal: