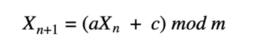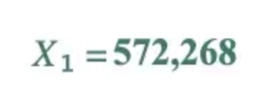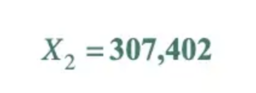(another ethical issue) |
|||
| (5 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | <b><font size="+4">Random Number In Modern Computer</font></b> | |
| − | = Random Number | + | |
[[File:Aaaaaaa.png|1024px|thumbnail|center]] | [[File:Aaaaaaa.png|1024px|thumbnail|center]] | ||
| − | |||
| − | |||
| − | = | + | <b><font size="+3">Introduction</font></b> |
| − | + | Randomness is not something that truly exists very often in the natural world. Things tend to obey laws that make interactions predictable. However, sometimes it is important to be able to create a random number. Humans have been interested in generating randomness for thousands of years. Ancient dice have been dug up and discovered that belonged to civilizations long ago. Things like dice or coins have been used by people to make decisions randomly as long as we have been around it seems. Random numbers are only something we have recently begun to understand and even more recently really began to need. Random numbers are constantly being used now in everyday life. Take cybersecurity as an example where data needs to be secured through encryption. Also online card games like blackjack are dependent on what numbers the dealer draws for the player. If the numbers are predictable the game does not work. Random numbers are also used all the time in modern video games, offering a way to generate new and unique worlds for a player. For these reason, it is important to create randomness. But mathematics and numbers are typically thought of as anything but random, and follow strict rules around changing them. For this reason, creating randomness is a unique challenge seen in modern mathematics that has been approached with several different unique strategies. | |
| − | |||
| + | <b><font size="+3">Method</font></b> | ||
| − | + | Almost all random number generation involve the use of some sort of seed to create the number. A seed is a number that is given and put into an algorithm to generate a random number. Then, the newly generated number is used as the seed for the next number. Getting the initial seed is what makes this random. This can be done by using the current time, atmospheric noise, or some other source that can provide an unpredictable value. To give an example of how this might work, we will use the time to generate a seed. If you were to call on a random number generator at 11:38, the random number generator could use the current time to the millionth decimal place as a seed to create an unpredictable value that could not be replicated. | |
| − | + | There are two main types of RNG: pseudo RNG, and true RNG. Pseudo RNG means that the numbers generated follow some sort of pattern, and could theoretically be predicted. In most scenarios, this is not a big deal. For example in a video game like Mario Kart, if the item a player is going to get from a mystery box is technically predictable or follows a pattern, it does not matter too much as long as the player does not catch on and is having fun. In something like online gambling, however, any sort of predictability can caouse millions of dollars of damage. For this reason, sometimes true RNG is needed. True RNG is more complicated to do as it requires more instruments, but is more effective than pseudo RNG at creating unpredictable numbers. | |
| − | |||
| − | = | + | <b><font size="+3">True Random Generation In Computer</font></b> |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | A truly random generator could provide a random number that is almost impossible to predict. We will not explore the true random generation in detail, because it is not very related to mathematical methods. Generally, a traditional computer that only has the basic components cannot generate a true random number, it has to be obtained by a specific device. These devices will convert some phenomena into a number. Some examples of TRNG sources include atmospheric noise, time, and radioactive decay. | |
| − | + | Atmospheric noise uses processes occurring in the atmosphere for its RNG. Most often, it will capture the static generated by lighting flashes, which occur roughly 40 times per second. (Random.org is known to use atmospheric noise to generate random outcomes for all kinds of different scenarios). For time, the device will take the exact nanosecond when you click the mouse as a random number. There is also one kind of device that uses a method that harvests entropy to obtain a random number using radioactivity because nuclear decay is unpredictable. | |
| − | + | ||
| + | <b><font size="+3">Pseudo random number generation</font></b> | ||
| + | |||
| + | The PRNG relies on algorithms and programs to generate a number sequence that seems to be random. But since it is using a fixed way to produce those numbers, it could be reproduced and predicted. This is because computer hardware is purely logical, which means it cannot provide output without input and processing, and that is exactly how random numbers are obtain from. So, as suggested by the prefix “pseudo”, the sequence is not random, it just looks like it. The two main components of a PRNG are an initial value or seed, and a pre-set algorithm. It follows the next several steps: | ||
| + | # Receive a seed as the input; | ||
| + | # Generate a number according to the preset algorithm; | ||
| + | # Use the output as the input for the next computation; | ||
| + | # Repeat the process until a specific time or required length is achieved. | ||
| + | Pseudo-random generators are deterministic and periodic. Deterministic means that the algorithm will always produce the same sequence of numbers given a specific seed, periodic means after a certain amount of recursion, the algorithm will start to provide a repeated number. A good generator should have a large period. | ||
| + | |||
| + | Here are two examples of popular random generation algorithm that are currently used: | ||
| + | |||
| + | |||
| + | <b><font size="+2"> Linear Congruential Algorithm</font></b> | ||
| + | |||
| + | One algorithm used for pseudo-RNG is the linear congruential algorithm shown below. | ||
[[File:Formula11.png|256px|frameless|center]] | [[File:Formula11.png|256px|frameless|center]] | ||
| − | In this algorithm, Xn | + | In this algorithm, Xn is the seed, so X₀ would be our initial seed gathered from one of the random methods we discussed. In this formula a is the multiplier, c is the increment, and m is the modulus. Both a and c must be greater than 0 and less than m. This way, with a pseudo-random seed number, we can use this algorithm to continue to generate numbers that would be functionally random, as long as the multiplier, increment, and modulus are unknown. |
| − | For example, we let X₀ = 235, a = 2,398, c = 8,738, and m=1,000,000 | + | For example, we let X₀ = 235, a = 2,398, c = 8,738, and m=1,000,000. |
| − | + | Since we had the seed already, we can go into the next step, use the formula and finish the calculation. | |
[[File:Example11.png|1024px|frameless|center]] | [[File:Example11.png|1024px|frameless|center]] | ||
| − | 1,000,000 fits into 572,268 0 times, leaving a remainder of 572,268 | + | 1,000,000 fits into 572,268 0 times, leaving a remainder of 572,268. |
[[File:Example12.png|256px|frameless|center]] | [[File:Example12.png|256px|frameless|center]] | ||
| − | Our X₁ is 572,268, so to get our X₂, we just have to use our formula again | + | Our X₁ is 572,268, so to get our X₂, we just have to use our formula again. |
[[File:Example13.png|1024px|frameless|center]] | [[File:Example13.png|1024px|frameless|center]] | ||
1,000,000 fits into 1,372,307,402 1372 times, leaving a remainder of 307,402. | 1,000,000 fits into 1,372,307,402 1372 times, leaving a remainder of 307,402. | ||
[[File:Example14.png|256px|frameless|center]] | [[File:Example14.png|256px|frameless|center]] | ||
| − | + | By repeating these steps, we got the first 5 random numbers as follows: 572268, 307402, 158734, 652870, and 590998. They look pretty random, and that's how the algorithms work. | |
| + | |||
| + | |||
| + | <b><font size="+2"> Middle-Square Algorithm</font></b> | ||
| + | |||
| + | A second method of doing pseudo RNG is with a middle square generator. This method takes an input value or seed and squares it. The resulting number then has its middle digits extracted to be the same length as the original seed, and then this number is used as the next seed. For example, if our initial seed was 3592, we would square it to get 12,902,464. Because our initial seed was 4 digits long, we would drop the 12 at the start and 64 at the end of the number to get our next seed, 9024. This method of RNG does require our squared seed to have twice the number of digits of the initial number and requires the seed to have an even number of digits. By addingleading zeros to the square of the seed, we make sure that we have an even number of digits. In the case of a squared seed not having twice the digits (such as 25*25 = 625), we add zeros again is added to the squared number to obey the rule (0625). In the same line of thinking, a 0 can be added to a number with an odd number of digits to be even, for example, 525 would be changed to 0525. While this seems unnecessary because the value of the number is still the same, computers interpret them differently so it is important to be consistent in following these rules. | ||
| + | |||
| + | |||
| + | <b><font size="+3"> Comparison between True and Pseudo random generation</font></b> | ||
| + | |||
| + | [[File:Pixabay.png|1024px|thumbnail|picture from Pixabay]] | ||
| + | PRNGs have higher convenience since all you need is a computer and an algorithm, but a TRNG requires an external device that is costly and may need maintainance to be kept in working condition. However, for cybersecurity, the TRNG takes the cake. For a sequence of true random numbers, there is no relation between subsequent values besides the fact that they come from the same source of entropy, which makes TRNG numbers virtually impossible to predict, and therefore much safer defenses against cyber attacks. Another disadvantage for PRNGs is that they are deterministic; because each number in the sequence relies on previous ones, they are much easier to decrypt. | ||
| + | |||
| + | |||
| + | <b><font size="+3"> Conclusion and Application</font></b> | ||
| + | |||
| + | Randomness is one really important part of modern computers, and such feature has been used for multiple areas such as Games, Politics, Science, and Cryptography. For the game, the famous example is video games like Minecraft which need to randomly generate a world for players. Online gambling is also another example that has a high demand for randomness. As for science, static sampling is basically defined by randomness. Also, for scientific analysis in the real world, almost all data will contain noise, for example, an experiment that tests specific X-rays. To determine the likelihood that a detected signal represents a genuine signal, random number generation is required. This fact also applies to model simulation, where the real phenomena are affected by unpredictable processes, such as radio noise or day-to-day weather, these models can be constructed through random numbers. And actually, "automatic random number generators were first constructed to carry out a computer simulation of physical phenomena, notably simulation of neutron transport in nuclear fission". | ||
| + | |||
| + | A ubiquitous use of unpredictable random numbers is in cryptography, which underlies most of the schemes which attempt to provide security in modern communications. If a user wants to use an encryption algorithm, it is best that they select a random number as the key so that it is unpredictable for any potential attackers. Using some public or simple random number generator is not a good choice, here is an example: "imagine if a simple 32-bit linear congruential pseudo-random number generator of the type supplied with most programming languages (e.g., as the 'rand' or 'rnd' function) is used as a source of keys. There will only be some four billion possible values produced before the generator repeats itself. A suitably motivated adversary could simply test them all; this is practical as of 2010, using readily available computers. Even if a linear congruential RNG is used with 1000-bit parameters, it is a simple exercise in linear algebra to recover the modulus m, and the constants a and b, where the formula is mentioned above, given only five consecutive values." As a result, any published random sequence will not pass the cryptographic standard. This pushes the implementation of enterprise use of random number generators, many informed observers even believe every computer should have a way to generate truly random numbers. | ||
| + | |||
| + | <b><font size="+3"> Ethical Problems</font></b> | ||
| + | |||
| + | As we could see, mostly the random number is used for science and cryptography, there is no ethic problem of using for the former because randomness is just a process, the result we obtain is nothing strongly related with random number. However, cryptography is used in the encryption of our data. What stops an adversary from reverse enginnering the seed in PRNG and simply claiming that they just guessed the password? That is why this question of using true or pseudo random number generators lies on the developer. At what point is the security of the data encrypted by the company random enough? Especially in todays age where there is so much data being generated by users and collected, where should a developer place the line between the security of the true random number generators and the perfomance of pseudo ones? This choice is still in the hands of developers. The ethical choice also pushes for better algorithms to generate random numbers. | ||
| + | |||
| + | Another ethical issue with random number generation is that it can be used to manipulate the outcome of events, such as gambling or elections. For example, if a random number generator is not truly random, it can be manipulated to produce a specific sequence of numbers that is biased towards a particular outcome. This can lead to unfairness and lack of trust in the system that is using the random numbers. Additionally, if the random number generator is not properly implemented or is not tested for randomness, it can introduce bias or unpredictability into the system, which can have negative consequences for the individuals or entities that are relying on the random numbers. This can also lead to lack of trust in the system and raise concerns about the fairness and reliability of the results it produces. | ||
| + | |||
| + | <b><font size="+2"> Reference</font></b> | ||
| + | |||
| + | Wikimedia Foundation. (2022, November 20). Random number generation. Wikipedia. Retrieved November 29, 2022, from https://en.wikipedia.org/wiki/Random_number_generation | ||
| + | |||
| + | Team, T. T. (2021, January 12). History of random number generators & how they work. Tech Magazine. Retrieved November 29, 2022, from https://techpages.net/random-number-generators-technology/ | ||
| + | |||
| + | M. Haahr, True Random Number Service. (1998), RANDOM.ORG | ||
| − | + | A. Arobelidze, Random Number Generator: How Do Computers Generate Random Numbers? (2020), FreeCodeCamp.org | |
| − | + | V. Ravindran, Linear Congruential Generator (2019), Vish Ravindran Blog | |
| − | + | S. Pigeon, The Middle Square Method (Generating Random Sequences VIII) (2017), Harder, Better, Faster, Stronger | |
| − | + | E. Herzstein. (2021, January 30). How do computers generate random numbers? Medium. Retrieved November 29, 2022, from https://levelup.gitconnected.com/how-do-computers-generate-random-numbers-a72be65877f6#5e79 | |
Latest revision as of 20:49, 5 December 2022
Random Number In Modern Computer
Introduction
Randomness is not something that truly exists very often in the natural world. Things tend to obey laws that make interactions predictable. However, sometimes it is important to be able to create a random number. Humans have been interested in generating randomness for thousands of years. Ancient dice have been dug up and discovered that belonged to civilizations long ago. Things like dice or coins have been used by people to make decisions randomly as long as we have been around it seems. Random numbers are only something we have recently begun to understand and even more recently really began to need. Random numbers are constantly being used now in everyday life. Take cybersecurity as an example where data needs to be secured through encryption. Also online card games like blackjack are dependent on what numbers the dealer draws for the player. If the numbers are predictable the game does not work. Random numbers are also used all the time in modern video games, offering a way to generate new and unique worlds for a player. For these reason, it is important to create randomness. But mathematics and numbers are typically thought of as anything but random, and follow strict rules around changing them. For this reason, creating randomness is a unique challenge seen in modern mathematics that has been approached with several different unique strategies.
Method
Almost all random number generation involve the use of some sort of seed to create the number. A seed is a number that is given and put into an algorithm to generate a random number. Then, the newly generated number is used as the seed for the next number. Getting the initial seed is what makes this random. This can be done by using the current time, atmospheric noise, or some other source that can provide an unpredictable value. To give an example of how this might work, we will use the time to generate a seed. If you were to call on a random number generator at 11:38, the random number generator could use the current time to the millionth decimal place as a seed to create an unpredictable value that could not be replicated.
There are two main types of RNG: pseudo RNG, and true RNG. Pseudo RNG means that the numbers generated follow some sort of pattern, and could theoretically be predicted. In most scenarios, this is not a big deal. For example in a video game like Mario Kart, if the item a player is going to get from a mystery box is technically predictable or follows a pattern, it does not matter too much as long as the player does not catch on and is having fun. In something like online gambling, however, any sort of predictability can caouse millions of dollars of damage. For this reason, sometimes true RNG is needed. True RNG is more complicated to do as it requires more instruments, but is more effective than pseudo RNG at creating unpredictable numbers.
True Random Generation In Computer
A truly random generator could provide a random number that is almost impossible to predict. We will not explore the true random generation in detail, because it is not very related to mathematical methods. Generally, a traditional computer that only has the basic components cannot generate a true random number, it has to be obtained by a specific device. These devices will convert some phenomena into a number. Some examples of TRNG sources include atmospheric noise, time, and radioactive decay.
Atmospheric noise uses processes occurring in the atmosphere for its RNG. Most often, it will capture the static generated by lighting flashes, which occur roughly 40 times per second. (Random.org is known to use atmospheric noise to generate random outcomes for all kinds of different scenarios). For time, the device will take the exact nanosecond when you click the mouse as a random number. There is also one kind of device that uses a method that harvests entropy to obtain a random number using radioactivity because nuclear decay is unpredictable.
Pseudo random number generation
The PRNG relies on algorithms and programs to generate a number sequence that seems to be random. But since it is using a fixed way to produce those numbers, it could be reproduced and predicted. This is because computer hardware is purely logical, which means it cannot provide output without input and processing, and that is exactly how random numbers are obtain from. So, as suggested by the prefix “pseudo”, the sequence is not random, it just looks like it. The two main components of a PRNG are an initial value or seed, and a pre-set algorithm. It follows the next several steps:
- Receive a seed as the input;
- Generate a number according to the preset algorithm;
- Use the output as the input for the next computation;
- Repeat the process until a specific time or required length is achieved.
Pseudo-random generators are deterministic and periodic. Deterministic means that the algorithm will always produce the same sequence of numbers given a specific seed, periodic means after a certain amount of recursion, the algorithm will start to provide a repeated number. A good generator should have a large period.
Here are two examples of popular random generation algorithm that are currently used:
Linear Congruential Algorithm
One algorithm used for pseudo-RNG is the linear congruential algorithm shown below.
In this algorithm, Xn is the seed, so X₀ would be our initial seed gathered from one of the random methods we discussed. In this formula a is the multiplier, c is the increment, and m is the modulus. Both a and c must be greater than 0 and less than m. This way, with a pseudo-random seed number, we can use this algorithm to continue to generate numbers that would be functionally random, as long as the multiplier, increment, and modulus are unknown.
For example, we let X₀ = 235, a = 2,398, c = 8,738, and m=1,000,000. Since we had the seed already, we can go into the next step, use the formula and finish the calculation.
1,000,000 fits into 572,268 0 times, leaving a remainder of 572,268.
Our X₁ is 572,268, so to get our X₂, we just have to use our formula again.
1,000,000 fits into 1,372,307,402 1372 times, leaving a remainder of 307,402.
By repeating these steps, we got the first 5 random numbers as follows: 572268, 307402, 158734, 652870, and 590998. They look pretty random, and that's how the algorithms work.
Middle-Square Algorithm
A second method of doing pseudo RNG is with a middle square generator. This method takes an input value or seed and squares it. The resulting number then has its middle digits extracted to be the same length as the original seed, and then this number is used as the next seed. For example, if our initial seed was 3592, we would square it to get 12,902,464. Because our initial seed was 4 digits long, we would drop the 12 at the start and 64 at the end of the number to get our next seed, 9024. This method of RNG does require our squared seed to have twice the number of digits of the initial number and requires the seed to have an even number of digits. By addingleading zeros to the square of the seed, we make sure that we have an even number of digits. In the case of a squared seed not having twice the digits (such as 25*25 = 625), we add zeros again is added to the squared number to obey the rule (0625). In the same line of thinking, a 0 can be added to a number with an odd number of digits to be even, for example, 525 would be changed to 0525. While this seems unnecessary because the value of the number is still the same, computers interpret them differently so it is important to be consistent in following these rules.
Comparison between True and Pseudo random generation
PRNGs have higher convenience since all you need is a computer and an algorithm, but a TRNG requires an external device that is costly and may need maintainance to be kept in working condition. However, for cybersecurity, the TRNG takes the cake. For a sequence of true random numbers, there is no relation between subsequent values besides the fact that they come from the same source of entropy, which makes TRNG numbers virtually impossible to predict, and therefore much safer defenses against cyber attacks. Another disadvantage for PRNGs is that they are deterministic; because each number in the sequence relies on previous ones, they are much easier to decrypt.
Conclusion and Application
Randomness is one really important part of modern computers, and such feature has been used for multiple areas such as Games, Politics, Science, and Cryptography. For the game, the famous example is video games like Minecraft which need to randomly generate a world for players. Online gambling is also another example that has a high demand for randomness. As for science, static sampling is basically defined by randomness. Also, for scientific analysis in the real world, almost all data will contain noise, for example, an experiment that tests specific X-rays. To determine the likelihood that a detected signal represents a genuine signal, random number generation is required. This fact also applies to model simulation, where the real phenomena are affected by unpredictable processes, such as radio noise or day-to-day weather, these models can be constructed through random numbers. And actually, "automatic random number generators were first constructed to carry out a computer simulation of physical phenomena, notably simulation of neutron transport in nuclear fission".
A ubiquitous use of unpredictable random numbers is in cryptography, which underlies most of the schemes which attempt to provide security in modern communications. If a user wants to use an encryption algorithm, it is best that they select a random number as the key so that it is unpredictable for any potential attackers. Using some public or simple random number generator is not a good choice, here is an example: "imagine if a simple 32-bit linear congruential pseudo-random number generator of the type supplied with most programming languages (e.g., as the 'rand' or 'rnd' function) is used as a source of keys. There will only be some four billion possible values produced before the generator repeats itself. A suitably motivated adversary could simply test them all; this is practical as of 2010, using readily available computers. Even if a linear congruential RNG is used with 1000-bit parameters, it is a simple exercise in linear algebra to recover the modulus m, and the constants a and b, where the formula is mentioned above, given only five consecutive values." As a result, any published random sequence will not pass the cryptographic standard. This pushes the implementation of enterprise use of random number generators, many informed observers even believe every computer should have a way to generate truly random numbers.
Ethical Problems
As we could see, mostly the random number is used for science and cryptography, there is no ethic problem of using for the former because randomness is just a process, the result we obtain is nothing strongly related with random number. However, cryptography is used in the encryption of our data. What stops an adversary from reverse enginnering the seed in PRNG and simply claiming that they just guessed the password? That is why this question of using true or pseudo random number generators lies on the developer. At what point is the security of the data encrypted by the company random enough? Especially in todays age where there is so much data being generated by users and collected, where should a developer place the line between the security of the true random number generators and the perfomance of pseudo ones? This choice is still in the hands of developers. The ethical choice also pushes for better algorithms to generate random numbers.
Another ethical issue with random number generation is that it can be used to manipulate the outcome of events, such as gambling or elections. For example, if a random number generator is not truly random, it can be manipulated to produce a specific sequence of numbers that is biased towards a particular outcome. This can lead to unfairness and lack of trust in the system that is using the random numbers. Additionally, if the random number generator is not properly implemented or is not tested for randomness, it can introduce bias or unpredictability into the system, which can have negative consequences for the individuals or entities that are relying on the random numbers. This can also lead to lack of trust in the system and raise concerns about the fairness and reliability of the results it produces.
Reference
Wikimedia Foundation. (2022, November 20). Random number generation. Wikipedia. Retrieved November 29, 2022, from https://en.wikipedia.org/wiki/Random_number_generation
Team, T. T. (2021, January 12). History of random number generators & how they work. Tech Magazine. Retrieved November 29, 2022, from https://techpages.net/random-number-generators-technology/
M. Haahr, True Random Number Service. (1998), RANDOM.ORG
A. Arobelidze, Random Number Generator: How Do Computers Generate Random Numbers? (2020), FreeCodeCamp.org
V. Ravindran, Linear Congruential Generator (2019), Vish Ravindran Blog
S. Pigeon, The Middle Square Method (Generating Random Sequences VIII) (2017), Harder, Better, Faster, Stronger
E. Herzstein. (2021, January 30). How do computers generate random numbers? Medium. Retrieved November 29, 2022, from https://levelup.gitconnected.com/how-do-computers-generate-random-numbers-a72be65877f6#5e79