| (28 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| + | --[[User:Student33MA279F22|Student33MA279F22]] ([[User talk:Student33MA279F22|talk]]) 17:18, 22 November 2022 (EST) | ||
| + | |||
'''Introduction''' | '''Introduction''' | ||
| − | Pi is possibly the most famous constant in mathematics. | + | Pi is possibly the most famous constant in mathematics. For thousands of years it has been a focus of mathematicians around the world. The earliest civilizations had a more limited understanding of mathematics than we have today but their rescillience lead to interesting solutions. Pi was originally held to be a rational number as there was no understanding of the possibility of irrational numbers. At a certain point it was discovered that its digits could extend forever and ways to calculate these digits became an area of discovery. There is a lot to consider throughout this history and even today. How many digits are necessary to know? Does the precision matter? Is there a best way to calculate the digits? Some questions relating to pi can be quite subjective but ultimately its objective value is of great importance to our understanding of the world and many physically practical applications. |
| − | |||
'''Basic Approximations''' | '''Basic Approximations''' | ||
| − | + | Fundamentally, π is just the ratio between a circle's circumference and its diameter: c = πd. So you can estimate π by taking a circle, measuring it, and dividing the circumference by the diameter. One variation of this is to roll a wheel out on a road many times--the distance traveled by the wheel will be the circumference * the number of rotations taken by the wheel. The success of a pure measuring method will depend on the perfectness of your circle and the precision of your measuring tools. | |
| − | + | ||
| − | + | ||
| − | - | + | |
| − | ' | + | Using rough approximation methods like this, some ancients initially thought that π = 22/7 (3.14285). However, it was later discovered that π is an irrational number, meaning it can't be represented by any fraction p/q where p and q are both integers. In order to determine π with a higher accuracy than simple measurement can achieve, mathematical calculation methods are needed. |
| − | + | By putting shapes whose area and perimeter were easily calculatable both inside and outside of a circle, early mathematicians were able to confidently know that pi was between the values of 3 and 4. Their methods were rarely significantly accurate but it is worth mentioning that it was definitively known that 3 < π < 4. | |
| − | |||
| − | + | '''Early Calculation''' | |
| − | + | ||
| + | In some of the earliest historical records known of pi, it was recorded to be somewhere roughly between 3 and 4. Specifically, the Babylonians nearly 4,000 years ago seem to have believed pi was 25/8 or 3.125. The Egyptians (at around the same time) noted the pi was (16/9)^2 or roughly 3.16. The most well-known early algorithm for computing pi is popularly known from the mathematician Archimedes (and a similar, iterative method was used in China known as Liu Hiu's Pi Algorithm). Archimedes knew that pi was described as the ratio of a circle's circumference to its diameter and to him the most significant limiting factor in calculating pi was knowing the exact circumference of some theoretical circle defined by a known radius. He could however find a close approximation by creating polygons both inside and outside the circle with known side lengths to calculate pi. This grew ever closer to pi the more sides were added to these polygons but took a significant amount of work. There is a famous example of a man who dedicated decades to the calculation of pi using this method, his name was Ludolph van Ceulen. He calculated pi up to 35 places using this method and when he died the digits for his upper and lower bounds of pi (from the inner and outer polygons around the circle in the approximation) were inscribed on his tombstone. Considering how many digits are actually necessary for calculations, especially at his time, this is perhaps an ethically questionable use of a life (or a significant amount of one). | ||
| − | |||
| − | |||
| − | |||
| − | |||
'''Modern Calculation''' | '''Modern Calculation''' | ||
| − | - | + | Today any computer or calculator can calculate the digits of pi fairly quickly (up to the limitations of the hardware), and there's even special-purpose software designed to calculate it exceptionally fast. Programs with names like QuickPi and PiFast compete to calculate the most digits of pi in the least amount of time. |
| − | - | + | |
| − | + | There are many methods to calculate pi, but the beginning of modern calculation was likely the discovery of calculus and infinite series which aided in manual computation. Newton is credited as the one who discovered the generalized binomial theorem which he used in conjunction with calculus to create his infinite series based on arcsin to calculate pi. He said at the time, "I am ashamed to tell you to how many figures I carried these computations, having no other business at the time." The intuition behind Newton's method is that he calculated part of the area of the unit circle (which has an area of π) and solved for π. He discovered that the binomial theorem could apply to non-integer powers so by representing this area as an integral of the binomial theorem's expansion he had an infinite series which converged to some multiple of pi which was relatively easy for him to solve by hand. | |
| − | + | ||
| + | To elaborate on what Newton did, this is the equation for a unit circle: | ||
| + | |||
| + | <math> | ||
| + | y^2+x^2=1 | ||
| + | </math> | ||
| + | |||
| + | This can be rearranged to form a binomial of power <math>\frac{1}{2}</math>: | ||
| + | |||
| + | <math> | ||
| + | y=(1-x^2)^{\frac{1}{2}} | ||
| + | </math> | ||
| + | |||
| + | Newton's realization that the binomial theorem holds for non-integer values and that this resulted in an infinite series lead him to attempt to integrate the expansion. Integrating from 0 to 1 was <math>\frac{\pi}{4}</math> which could easily be rearranged to solve for π. The following is an expansion of the binomial up to four terms: | ||
| + | |||
| + | <math> | ||
| + | (1-x^2)^{\frac{1}{2}} = 1 - \frac{x^2}{2} - \frac{x^4}{8} - \frac{x^6}{16}\,... | ||
| + | </math> | ||
| + | |||
| + | Integrating this series from 0 to 1 is then trivial. | ||
| + | |||
| + | Some people wonder how many digits of pi are currently known, but there isn't really an answer to this question, because thanks to the discovery of closed-form calculations, the answer is technically "all of them" (we can compute any given digit for you right now). The computation of a digit of pi without having to know preceding digits is referred to as [https://en.wikipedia.org/wiki/Approximations_of_%CF%80#Digit_extraction_methods digit extraction]. The fastest formula currently known is Fabrice Bellard's, which can compute the nth digit of pi in O(n^2) time. | ||
| + | |||
| + | The fastest known algorithms used by computers to calculate pi in the traditional sense exist in both iterative and infinite series forms. Initially iterative algorithms were thought to be the fastest way to calculate pi but more recently rapidly converging infinite series have been discovered which are about as fast as iterative algorithms. To be clear on the meanings here, an iterative algorithm begins with a specified value (or set of specified values), calculates some value, then feeds that calculated value back into the formula as if it were the initial value. Ultimately this will convergence by repeatedly using previously calculated values. The infinite series algorithms may be represented as a summation where each term is individually calculable, not dependent on previous terms. The results from each term in the infinite series are summed together. | ||
| + | |||
| + | For interesting reading, the book Contact by Carl Sagan is a science fiction book which bases a reasonable amount of the plot around pi and its computation. | ||
| + | |||
'''Interesting Calculation Methods''' | '''Interesting Calculation Methods''' | ||
| − | One interesting way to calculate π is by throwing a bunch of sticks on the ground, on a grid of parallel lines. By using the length of a stick, the size of the gaps between the lines, and the number of sticks that are crossing a line, we can find an estimate for π. This experiment is called Buffon’s needle, and you can try it for yourself | + | One interesting way to calculate π is by throwing a bunch of sticks on the ground, on a grid of parallel lines. By using the length of a stick, the size of the gaps between the lines, and the number of sticks that are crossing a line, we can find an estimate for π. This experiment is called Buffon’s needle, and you can try it for yourself [https://ogden.eu/pi/ here]. |
| − | + | [[File:BuffonsNeedle.png|400x400px|frameless]] | |
| − | If we normalize the distance between lines to 1, we can draw each stick as follows, where D is the distance of its midpoint from the nearest line and θ is the angle of the stick from parallel. The needle will hit the line if D ≤ 1/ | + | If we normalize the distance between lines to 1, we can draw each stick as follows, where D is the distance of its midpoint from the nearest line and θ is the angle of the stick from parallel. The needle will hit the line if D ≤ (1/2)sin(θ). |
| − | + | [[File:BuffonsNeedleTrig.png|434x188px|frameless]] | |
| − | In order to determine how often this happens, we can plot 1/ | + | In order to determine how often this happens, we can plot (1/2)sin(θ) on a graph. As you can see, D can range from 0 to ½ and θ can range from 0 to π radians. The blue area of the graph is where D ≤ (1/2)sin(θ). So in order to find the probability that D ≤ (1/2)sin(θ), we can take the area of the blue curve divided by the area of the rectangle of total possibilities. |
| − | + | [[File:BuffonsNeedleBlueCurve.png|434x188px|frameless]] | |
The area under the blue curve, found using integration, is 1, and the area of the enclosing rectangle is π/2. So (needles touching a line)/(total needles) ≈ 1/(π/2) = 2/π. We can input our real data and rearrange this equation to approximate pi. This kind of calculation isn't very practical, but if you get too frustrated with infinite series and calculus then we've found throwing sticks on the ground to be quite cathartic. | The area under the blue curve, found using integration, is 1, and the area of the enclosing rectangle is π/2. So (needles touching a line)/(total needles) ≈ 1/(π/2) = 2/π. We can input our real data and rearrange this equation to approximate pi. This kind of calculation isn't very practical, but if you get too frustrated with infinite series and calculus then we've found throwing sticks on the ground to be quite cathartic. | ||
| Line 52: | Line 72: | ||
'''Applications''' | '''Applications''' | ||
| − | + | Knowing pi is valuable any time you want to calculate the volume or surface area of a cylinder or sphere. For example, a water bottle manufacturer who wants to know how much metal they need to make a water bottle with specified dimensions can use pi to calculate the volume of the bottle. They could also use it to find the surface area of the bottle, to determine how much paint they need to color it. In a similar vein, a construction company might use pi to figure out how much concrete they need for a circular pillar. | |
| − | - | + | |
| − | + | Another use-case for pi is related to circular velocity--for example, determining how fast a piston connected to the wheels on a train is moving. It is also useful in many branches of science, from calculating the wavelength and amplitude of electromagnetic waves based on the frequency, the motion of objects in astronomical bodies, | |
| − | - | + | |
| + | In practice, most applications of pi require no more than a few digits of precision, and even things like the calculation of orbits and trajectories for interplanetary navigation need no more than dozens of digits. People have calculated trillions of digits of pi not for any particular use but just because they can. | ||
| + | |||
| + | |||
| + | '''Practical Approximation of Pi''' | ||
| + | |||
| + | The current record for the number of digits of pi calculated is 100 trillion digits, so how many digits of pi are necessary for practical use ? For most applications, not many. | ||
| + | |||
| + | The most digits that are commonly used for a practical purpose is 15 digits of pi. NASA uses this approximation of pi for calculations regarding interplanetary navigation. Now, you may be asking, “We have trillions of digits of pi, so why not use more of them for more accurate results?” The reason is that it's extreme overkill. To demonstrate this, let's calculate the circumference of the earth. The circumference of the earth is roughly 24,900 miles, and if you were to calculate the circumference of the earth using 15 digits of pi, and compare it to the circumference using the 62.8 trillion digits, the amount of error associated with using the 15 digits of pi would amount to the diameter of a molecule. It’s an extremely negligible difference! While we can use more exact approximations of pi, it is rarely practical to do so. | ||
| + | |||
| + | Beyond these uses for practical applications, the approximation of pi is also used for other reasons. One of the most famous ways we use more digits of pi is to memorize them! Many people have set out to memorize as many of the digits of pi as they can either for fun, or to break records. The current world record for number of digits of pi is 67,890 digits by Lu Chao in 2005. Although these challenges don’t serve a practical purpose, they are entertaining and serve to test the limits of our brains to memorize information. | ||
| + | |||
| + | The approximation of pi is also used as a benchmark to test the accuracy, performance, and stability of computers. SuperPI is a common benchmark that uses the Gauss-Legendre algorithm to calculate pi up to 32 million digits. The current record for number of digits of pi calculated, 100 trillion, was calculated for the purpose of benchmarking by Google, to test their Google Cloud platform. | ||
| + | |||
| + | |||
| + | '''Indiana Pi Bill''' | ||
| + | |||
| + | Since pi is applicable in many different fields in STEM, it is important that pi is calculated as accurately as needed. It isn’t practical to use millions of digits to calculate the area of a circle for your high school geometry class, but it is also potentially dangerous to calculate a moon landing using only 4 digits. | ||
| + | |||
| + | One of the most famous ethical dilemmas regarding the approximation of pi happened right here in Indiana! The Indiana Pi Bill was a bill proposed to the Indiana General Assembly which claimed to have a method to square the circle. This is a challenge to create a square with the area of a circle by using a finite number of steps and only a compass and straightedge. This has been proved impossible, but there are many mathematicians that will still try to successfully square the circle. One of these mathematicians is Edward J. Goodwin, who, in 1894, believed he had found a solution to this problem. But the issue with his solution involved approximating pi to 3.2. He presented the bill to the Indiana House of Representatives, and they passed the bill unanimously. Upon learning that this bill passed in the House, Purdue University professor C. A. Waldo had talked to senators in the Indiana Senate and demonstrated how ludicrous the proposed bill was. The Indiana Senate then postponed the bill indefinitely and prevented Goodwin’s approximation of pi to 3.2 from being passed into Indiana law. | ||
| + | |||
| + | Had the bill passed into law, the state of Indiana would be allowed to use this “new mathematical truth” free of charge, but other states would have to pay royalties to Goodwin to use this new method for squaring the circle. Potentially, Goodwin’s bill could have derailed Indiana’s education system by legally defining pi as 3.2 and caused great confusion in the schools of Indiana as they were using imprecise approximations of pi. Pi rounded to 3.2 has a significant amount of rounding error and would impact work that requires an approximation of pi accurate to 2 digits. | ||
| + | |||
| + | |||
| + | '''Ethical Implications''' | ||
| + | |||
| + | The Indiana Pi bill and a life spent calculating pi are a couple obvious examples of the ethical implications of the computation of pi. Beyond those, the Indiana Pi bill highlights a more significant ethical implication with pi in that the misrepresentation of its calculation is akin to lying. Rounding pi is also a controversial issue. Perhaps hiding the fact that it is irrational by rounding pi to 3 would help students more easily understand calculations involving pi but it might not be best for their understanding the concept. | ||
| + | |||
| + | Other than education, the major ethical implications of the computation of pi involve, again, its accuracy for other applications. Important engineering projects may cause harm if bad versions of pi are used. | ||
| + | |||
'''References''' | '''References''' | ||
| − | - | + | Atkinson, N. (2015, December 23). Happy pi day: 5 ways NASA uses pi. Universe Today. Retrieved November 28, 2022, from https://www.universetoday.com/110331/happy-pi-day-5-ways-nasa-uses-pi/#:~:text=In%20basic%20mathematics%2C%20Pi%20is,flight%2C%20to%20name%20a%20few |
| + | |||
| + | Buffon's Needle. Buffon's Needle, MSTE, University of Illinois. (n.d.). Retrieved November 28, 2022, from https://mste.illinois.edu/activity/buffon/ | ||
| + | |||
| + | The indiana pi bill and the attempt to redefine mathematics through Legislative Fiat. Commonplace Fun Facts. (2020, August 6). Retrieved November 28, 2022, from https://commonplacefacts.com/2020/05/17/the-indiana-pi-bill-and-the-attempt-to-redefine-mathematics-through-legislative-fiat/ | ||
| + | |||
| + | Lewis, T. (2015, March 13). Pi, anyone? the secret to memorizing tens of thousands of digits. LiveScience. Retrieved November 28, 2022, from https://www.livescience.com/50134-pi-day-memory-experts.html | ||
| + | |||
| + | Martinović, G., Balen, J., & Rimac-Drlje, S. (2010, July 29). Impact of the host operating systems on virtual machine ... - IEEE xplore. Impact of the host operating systems on virtual machine performance. Retrieved November 29, 2022, from https://ieeexplore.ieee.org/document/5533473 | ||
| + | |||
| + | Muller, D. (2021). The Discovery That Transformed Pi. YouTube. YouTube. Retrieved December 7, 2022, from https://www.youtube.com/watch?v=gMlf1ELvRzc. | ||
| + | |||
| + | NASA/JPL Edu. (2022, October 25). How many decimals of pi do we really need? - edu news. NASA. Retrieved November 28, 2022, from https://www.jpl.nasa.gov/edu/news/2016/3/16/how-many-decimals-of-%20pi-do-we-really-need/ | ||
| + | |||
| + | O'Connor, J. J., & Robertson, E. F. (2009, April). Ludolph van Ceulen - Biography. Maths History. Retrieved November 28, 2022, from https://mathshistory.st-andrews.ac.uk/Biographies/Van_Ceulen/ | ||
| + | |||
| + | Ogden, T. (2011, March 14). Pickup sticks & pi. Atom. Retrieved November 28, 2022, from https://ogden.eu/pi/ | ||
| + | |||
| + | Pilastro, E. (2022, March 14). New value of pi calculated by Swiss university at over 62 trillion digits. Guinness World Records. Retrieved November 28, 2022, from https://www.guinnessworldrecords.com/news/2022/3/new-value-of-pi-calculated-by-swiss-university-at-over-62-billion-digits-694748 | ||
| + | |||
| + | Wikimedia Foundation. (2022, November 10). Approximations of π. Wikipedia. Retrieved November 28, 2022, from https://en.wikipedia.org/wiki/Approximations_of_%CF%80 | ||
| + | |||
| + | Wikimedia Foundation. (2022, November 10). Approximations of π. Wikipedia. Retrieved November 28, 2022, from https://en.wikipedia.org/wiki/Approximations_of_%CF%80#Digit_extraction_methods | ||
| + | |||
| + | Wikimedia Foundation. (2022, November 28). Chronology of computation of π. Wikipedia. Retrieved November 28, 2022, from https://en.wikipedia.org/wiki/Chronology_of_computation_of_%CF%80 | ||
| + | |||
| + | Wikimedia Foundation. (2022, November 28). Pi. Wikipedia. Retrieved November 28, 2022, from https://en.wikipedia.org/wiki/Pi | ||
| − | + | Wikimedia Foundation. (2022, September 24). Liu Hui's π algorithm. Wikipedia. Retrieved November 28, 2022, from https://en.wikipedia.org/wiki/Liu_Hui%27s_%CF%80_algorithm | |
| − | + | ||
| − | https://en.wikipedia.org/wiki/Liu_Hui% | + | |
| − | + | ||
| − | + | ||
| − | + | ||
[[Category:MA279Fall2022Swanson]] | [[Category:MA279Fall2022Swanson]] | ||
Latest revision as of 10:22, 8 December 2022
--Student33MA279F22 (talk) 17:18, 22 November 2022 (EST)
Introduction
Pi is possibly the most famous constant in mathematics. For thousands of years it has been a focus of mathematicians around the world. The earliest civilizations had a more limited understanding of mathematics than we have today but their rescillience lead to interesting solutions. Pi was originally held to be a rational number as there was no understanding of the possibility of irrational numbers. At a certain point it was discovered that its digits could extend forever and ways to calculate these digits became an area of discovery. There is a lot to consider throughout this history and even today. How many digits are necessary to know? Does the precision matter? Is there a best way to calculate the digits? Some questions relating to pi can be quite subjective but ultimately its objective value is of great importance to our understanding of the world and many physically practical applications.
Basic Approximations
Fundamentally, π is just the ratio between a circle's circumference and its diameter: c = πd. So you can estimate π by taking a circle, measuring it, and dividing the circumference by the diameter. One variation of this is to roll a wheel out on a road many times--the distance traveled by the wheel will be the circumference * the number of rotations taken by the wheel. The success of a pure measuring method will depend on the perfectness of your circle and the precision of your measuring tools.
Using rough approximation methods like this, some ancients initially thought that π = 22/7 (3.14285). However, it was later discovered that π is an irrational number, meaning it can't be represented by any fraction p/q where p and q are both integers. In order to determine π with a higher accuracy than simple measurement can achieve, mathematical calculation methods are needed.
By putting shapes whose area and perimeter were easily calculatable both inside and outside of a circle, early mathematicians were able to confidently know that pi was between the values of 3 and 4. Their methods were rarely significantly accurate but it is worth mentioning that it was definitively known that 3 < π < 4.
Early Calculation
In some of the earliest historical records known of pi, it was recorded to be somewhere roughly between 3 and 4. Specifically, the Babylonians nearly 4,000 years ago seem to have believed pi was 25/8 or 3.125. The Egyptians (at around the same time) noted the pi was (16/9)^2 or roughly 3.16. The most well-known early algorithm for computing pi is popularly known from the mathematician Archimedes (and a similar, iterative method was used in China known as Liu Hiu's Pi Algorithm). Archimedes knew that pi was described as the ratio of a circle's circumference to its diameter and to him the most significant limiting factor in calculating pi was knowing the exact circumference of some theoretical circle defined by a known radius. He could however find a close approximation by creating polygons both inside and outside the circle with known side lengths to calculate pi. This grew ever closer to pi the more sides were added to these polygons but took a significant amount of work. There is a famous example of a man who dedicated decades to the calculation of pi using this method, his name was Ludolph van Ceulen. He calculated pi up to 35 places using this method and when he died the digits for his upper and lower bounds of pi (from the inner and outer polygons around the circle in the approximation) were inscribed on his tombstone. Considering how many digits are actually necessary for calculations, especially at his time, this is perhaps an ethically questionable use of a life (or a significant amount of one).
Modern Calculation
Today any computer or calculator can calculate the digits of pi fairly quickly (up to the limitations of the hardware), and there's even special-purpose software designed to calculate it exceptionally fast. Programs with names like QuickPi and PiFast compete to calculate the most digits of pi in the least amount of time.
There are many methods to calculate pi, but the beginning of modern calculation was likely the discovery of calculus and infinite series which aided in manual computation. Newton is credited as the one who discovered the generalized binomial theorem which he used in conjunction with calculus to create his infinite series based on arcsin to calculate pi. He said at the time, "I am ashamed to tell you to how many figures I carried these computations, having no other business at the time." The intuition behind Newton's method is that he calculated part of the area of the unit circle (which has an area of π) and solved for π. He discovered that the binomial theorem could apply to non-integer powers so by representing this area as an integral of the binomial theorem's expansion he had an infinite series which converged to some multiple of pi which was relatively easy for him to solve by hand.
To elaborate on what Newton did, this is the equation for a unit circle:
$ y^2+x^2=1 $
This can be rearranged to form a binomial of power $ \frac{1}{2} $:
$ y=(1-x^2)^{\frac{1}{2}} $
Newton's realization that the binomial theorem holds for non-integer values and that this resulted in an infinite series lead him to attempt to integrate the expansion. Integrating from 0 to 1 was $ \frac{\pi}{4} $ which could easily be rearranged to solve for π. The following is an expansion of the binomial up to four terms:
$ (1-x^2)^{\frac{1}{2}} = 1 - \frac{x^2}{2} - \frac{x^4}{8} - \frac{x^6}{16}\,... $
Integrating this series from 0 to 1 is then trivial.
Some people wonder how many digits of pi are currently known, but there isn't really an answer to this question, because thanks to the discovery of closed-form calculations, the answer is technically "all of them" (we can compute any given digit for you right now). The computation of a digit of pi without having to know preceding digits is referred to as digit extraction. The fastest formula currently known is Fabrice Bellard's, which can compute the nth digit of pi in O(n^2) time.
The fastest known algorithms used by computers to calculate pi in the traditional sense exist in both iterative and infinite series forms. Initially iterative algorithms were thought to be the fastest way to calculate pi but more recently rapidly converging infinite series have been discovered which are about as fast as iterative algorithms. To be clear on the meanings here, an iterative algorithm begins with a specified value (or set of specified values), calculates some value, then feeds that calculated value back into the formula as if it were the initial value. Ultimately this will convergence by repeatedly using previously calculated values. The infinite series algorithms may be represented as a summation where each term is individually calculable, not dependent on previous terms. The results from each term in the infinite series are summed together.
For interesting reading, the book Contact by Carl Sagan is a science fiction book which bases a reasonable amount of the plot around pi and its computation.
Interesting Calculation Methods
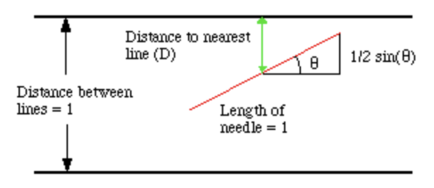
One interesting way to calculate π is by throwing a bunch of sticks on the ground, on a grid of parallel lines. By using the length of a stick, the size of the gaps between the lines, and the number of sticks that are crossing a line, we can find an estimate for π. This experiment is called Buffon’s needle, and you can try it for yourself here.
If we normalize the distance between lines to 1, we can draw each stick as follows, where D is the distance of its midpoint from the nearest line and θ is the angle of the stick from parallel. The needle will hit the line if D ≤ (1/2)sin(θ).
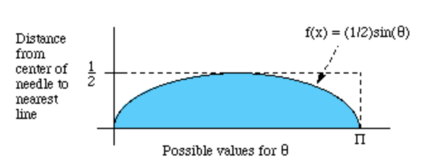
In order to determine how often this happens, we can plot (1/2)sin(θ) on a graph. As you can see, D can range from 0 to ½ and θ can range from 0 to π radians. The blue area of the graph is where D ≤ (1/2)sin(θ). So in order to find the probability that D ≤ (1/2)sin(θ), we can take the area of the blue curve divided by the area of the rectangle of total possibilities.
The area under the blue curve, found using integration, is 1, and the area of the enclosing rectangle is π/2. So (needles touching a line)/(total needles) ≈ 1/(π/2) = 2/π. We can input our real data and rearrange this equation to approximate pi. This kind of calculation isn't very practical, but if you get too frustrated with infinite series and calculus then we've found throwing sticks on the ground to be quite cathartic.
Applications
Knowing pi is valuable any time you want to calculate the volume or surface area of a cylinder or sphere. For example, a water bottle manufacturer who wants to know how much metal they need to make a water bottle with specified dimensions can use pi to calculate the volume of the bottle. They could also use it to find the surface area of the bottle, to determine how much paint they need to color it. In a similar vein, a construction company might use pi to figure out how much concrete they need for a circular pillar.
Another use-case for pi is related to circular velocity--for example, determining how fast a piston connected to the wheels on a train is moving. It is also useful in many branches of science, from calculating the wavelength and amplitude of electromagnetic waves based on the frequency, the motion of objects in astronomical bodies,
In practice, most applications of pi require no more than a few digits of precision, and even things like the calculation of orbits and trajectories for interplanetary navigation need no more than dozens of digits. People have calculated trillions of digits of pi not for any particular use but just because they can.
Practical Approximation of Pi
The current record for the number of digits of pi calculated is 100 trillion digits, so how many digits of pi are necessary for practical use ? For most applications, not many.
The most digits that are commonly used for a practical purpose is 15 digits of pi. NASA uses this approximation of pi for calculations regarding interplanetary navigation. Now, you may be asking, “We have trillions of digits of pi, so why not use more of them for more accurate results?” The reason is that it's extreme overkill. To demonstrate this, let's calculate the circumference of the earth. The circumference of the earth is roughly 24,900 miles, and if you were to calculate the circumference of the earth using 15 digits of pi, and compare it to the circumference using the 62.8 trillion digits, the amount of error associated with using the 15 digits of pi would amount to the diameter of a molecule. It’s an extremely negligible difference! While we can use more exact approximations of pi, it is rarely practical to do so.
Beyond these uses for practical applications, the approximation of pi is also used for other reasons. One of the most famous ways we use more digits of pi is to memorize them! Many people have set out to memorize as many of the digits of pi as they can either for fun, or to break records. The current world record for number of digits of pi is 67,890 digits by Lu Chao in 2005. Although these challenges don’t serve a practical purpose, they are entertaining and serve to test the limits of our brains to memorize information.
The approximation of pi is also used as a benchmark to test the accuracy, performance, and stability of computers. SuperPI is a common benchmark that uses the Gauss-Legendre algorithm to calculate pi up to 32 million digits. The current record for number of digits of pi calculated, 100 trillion, was calculated for the purpose of benchmarking by Google, to test their Google Cloud platform.
Indiana Pi Bill
Since pi is applicable in many different fields in STEM, it is important that pi is calculated as accurately as needed. It isn’t practical to use millions of digits to calculate the area of a circle for your high school geometry class, but it is also potentially dangerous to calculate a moon landing using only 4 digits.
One of the most famous ethical dilemmas regarding the approximation of pi happened right here in Indiana! The Indiana Pi Bill was a bill proposed to the Indiana General Assembly which claimed to have a method to square the circle. This is a challenge to create a square with the area of a circle by using a finite number of steps and only a compass and straightedge. This has been proved impossible, but there are many mathematicians that will still try to successfully square the circle. One of these mathematicians is Edward J. Goodwin, who, in 1894, believed he had found a solution to this problem. But the issue with his solution involved approximating pi to 3.2. He presented the bill to the Indiana House of Representatives, and they passed the bill unanimously. Upon learning that this bill passed in the House, Purdue University professor C. A. Waldo had talked to senators in the Indiana Senate and demonstrated how ludicrous the proposed bill was. The Indiana Senate then postponed the bill indefinitely and prevented Goodwin’s approximation of pi to 3.2 from being passed into Indiana law.
Had the bill passed into law, the state of Indiana would be allowed to use this “new mathematical truth” free of charge, but other states would have to pay royalties to Goodwin to use this new method for squaring the circle. Potentially, Goodwin’s bill could have derailed Indiana’s education system by legally defining pi as 3.2 and caused great confusion in the schools of Indiana as they were using imprecise approximations of pi. Pi rounded to 3.2 has a significant amount of rounding error and would impact work that requires an approximation of pi accurate to 2 digits.
Ethical Implications
The Indiana Pi bill and a life spent calculating pi are a couple obvious examples of the ethical implications of the computation of pi. Beyond those, the Indiana Pi bill highlights a more significant ethical implication with pi in that the misrepresentation of its calculation is akin to lying. Rounding pi is also a controversial issue. Perhaps hiding the fact that it is irrational by rounding pi to 3 would help students more easily understand calculations involving pi but it might not be best for their understanding the concept.
Other than education, the major ethical implications of the computation of pi involve, again, its accuracy for other applications. Important engineering projects may cause harm if bad versions of pi are used.
References
Atkinson, N. (2015, December 23). Happy pi day: 5 ways NASA uses pi. Universe Today. Retrieved November 28, 2022, from https://www.universetoday.com/110331/happy-pi-day-5-ways-nasa-uses-pi/#:~:text=In%20basic%20mathematics%2C%20Pi%20is,flight%2C%20to%20name%20a%20few
Buffon's Needle. Buffon's Needle, MSTE, University of Illinois. (n.d.). Retrieved November 28, 2022, from https://mste.illinois.edu/activity/buffon/
The indiana pi bill and the attempt to redefine mathematics through Legislative Fiat. Commonplace Fun Facts. (2020, August 6). Retrieved November 28, 2022, from https://commonplacefacts.com/2020/05/17/the-indiana-pi-bill-and-the-attempt-to-redefine-mathematics-through-legislative-fiat/
Lewis, T. (2015, March 13). Pi, anyone? the secret to memorizing tens of thousands of digits. LiveScience. Retrieved November 28, 2022, from https://www.livescience.com/50134-pi-day-memory-experts.html
Martinović, G., Balen, J., & Rimac-Drlje, S. (2010, July 29). Impact of the host operating systems on virtual machine ... - IEEE xplore. Impact of the host operating systems on virtual machine performance. Retrieved November 29, 2022, from https://ieeexplore.ieee.org/document/5533473
Muller, D. (2021). The Discovery That Transformed Pi. YouTube. YouTube. Retrieved December 7, 2022, from https://www.youtube.com/watch?v=gMlf1ELvRzc.
NASA/JPL Edu. (2022, October 25). How many decimals of pi do we really need? - edu news. NASA. Retrieved November 28, 2022, from https://www.jpl.nasa.gov/edu/news/2016/3/16/how-many-decimals-of-%20pi-do-we-really-need/
O'Connor, J. J., & Robertson, E. F. (2009, April). Ludolph van Ceulen - Biography. Maths History. Retrieved November 28, 2022, from https://mathshistory.st-andrews.ac.uk/Biographies/Van_Ceulen/
Ogden, T. (2011, March 14). Pickup sticks & pi. Atom. Retrieved November 28, 2022, from https://ogden.eu/pi/
Pilastro, E. (2022, March 14). New value of pi calculated by Swiss university at over 62 trillion digits. Guinness World Records. Retrieved November 28, 2022, from https://www.guinnessworldrecords.com/news/2022/3/new-value-of-pi-calculated-by-swiss-university-at-over-62-billion-digits-694748
Wikimedia Foundation. (2022, November 10). Approximations of π. Wikipedia. Retrieved November 28, 2022, from https://en.wikipedia.org/wiki/Approximations_of_%CF%80
Wikimedia Foundation. (2022, November 10). Approximations of π. Wikipedia. Retrieved November 28, 2022, from https://en.wikipedia.org/wiki/Approximations_of_%CF%80#Digit_extraction_methods
Wikimedia Foundation. (2022, November 28). Chronology of computation of π. Wikipedia. Retrieved November 28, 2022, from https://en.wikipedia.org/wiki/Chronology_of_computation_of_%CF%80
Wikimedia Foundation. (2022, November 28). Pi. Wikipedia. Retrieved November 28, 2022, from https://en.wikipedia.org/wiki/Pi
Wikimedia Foundation. (2022, September 24). Liu Hui's π algorithm. Wikipedia. Retrieved November 28, 2022, from https://en.wikipedia.org/wiki/Liu_Hui%27s_%CF%80_algorithm