| (15 intermediate revisions by the same user not shown) | |||
| Line 37: | Line 37: | ||
<center> <math> F_n = \frac{1}{\sqrt{5}}[φ^n - (1 - φ)^n] </math> </center> | <center> <math> F_n = \frac{1}{\sqrt{5}}[φ^n - (1 - φ)^n] </math> </center> | ||
| − | This is known as Binet’s formula. The derivation of Binet’s formula involves some clever math involving infinite series. We wish to find a formula <math> F(x) </math> that yields the <math> x^{th}</math> Fibonacci number. To begin, we represent <math> F(x) </math> as a power series with coefficients equal to the <math> n^{th}</math> Fibonacci number: | + | This is known as Binet’s formula <sup>[https://artofproblemsolving.com/wiki/index.php?title=Binet%27s_Formula (10)]</sup>. The derivation of Binet’s formula involves some clever math involving infinite series. We wish to find a formula <math> F(x) </math> that yields the <math> x^{th}</math> Fibonacci number. To begin, we represent <math> F(x) </math> as a power series with coefficients equal to the <math> n^{th}</math> Fibonacci number: |
| − | <center> <math> F(x) = 0 \cdot x^0 + 1 \cdot x^1 + 1 \cdot x^2 + 2 \cdot x^3 + 5 \cdot x^4 + … + F_n \cdot x^n + … = \ | + | <center> <math> F(x) = 0 \cdot x^0 + 1 \cdot x^1 + 1 \cdot x^2 + 2 \cdot x^3 + 5 \cdot x^4 + … + F_n \cdot x^n + … = \Sigma_{n=0}^{\infty} F_n x^n = 0 + x + \Sigma_{n=2}^{\infty} F_n x^n </math> </center> |
| + | Next, we take the recursive relationship that defines the Fibonacci sequence and substitute for <math> F_n </math>: | ||
| + | <center> <math> F(x) = x + \Sigma_{n=2}^{\infty} (F_{n-1} + F_{n-2}) x^n = x + \Sigma_{n=2}^{\infty} F_{n-1} x^n + \Sigma_{n=2}^{\infty} F_{n-2} x^n </math> </center> | ||
| + | This expansion makes it clear why the first two terms of the sequence had to be removed from the infinite sum: otherwise <math> F_{n-2} </math> and <math> F_{n-1} </math> would not be defined, as <math> n </math> would be negative. | ||
| + | Consider the first sum containing <math> F_{n-1} </math>. It can be rewritten in terms of the original function <math> F(x) </math> by factoring out x: | ||
| + | <center> <math> \Sigma_{n=2}^{\infty} F_{n-1} x^n = x \Sigma_{n=2}^{\infty} F_{n-1} x^{n-1} = x [0 + \Sigma_{n=1}^{\infty} F_{n} x^{n}] = x F(x) </math> </center> | ||
| + | For the second sum containing <math> F_{n-2} </math> we may do the same thing by factoring out <math> x^2 </math> instead of <math> x </math>: | ||
| − | + | <center> <math> \Sigma_{n=2}^{\infty} F_{n-2} x^n = x^2 \Sigma_{n=2}^{\infty} F_{n-2} x^{n-2} = x^2 \Sigma_{n=0}^{\infty} F_{n} x^{n}] = x^2 F(x) </math> </center> | |
| − | + | ||
| − | + | ||
| + | With some basic algebra, the above expression can be solved for <math> F(x) </math>, yielding: | ||
| + | <center> <math> F(x) = \frac{x}{1 – x – x^2} </math></center> | ||
| + | At this point, it may still seem unclear as to how a formula for the Fibonacci series can be found from the above equation. The goal is to find a formula for the coefficients of the power series used to define <math> F(x) </math> in terms of <math> n </math>. Since the <math> n^{th} </math> coefficient of the power series is equal to the <math> n^{th} </math> Fibonacci number by construction, this will give an explicit formula for the Fibonacci numbers. | ||
| + | The way forward is to somehow express the new equation for <math> F(x) </math> as a well-known power series. First note that the quadratic polynomial in the denominator of <math> F(x) </math> is the same as that of the derivation of the golden ratio. <math> F(x) </math> can then be rewritten as: | ||
| + | |||
| + | <center> <math> F(x) = - \frac{x}{(x + \phi) (x + \frac{1}{\phi})} = \frac{1}{\sqrt{5}} (\frac{1}{1 - \phi x} - \frac{1}{1 - \frac{1}{\phi} x}) </math> </center> | ||
| + | |||
| + | The algebra invovled in obtaining the above equation is somewhat complicated, and involves using identies of the golden ratio like <math> \phi = \frac{1}{\phi} </math> as well as a technique called partial fractions. However, the equivalence of the above expression can be easily verified. | ||
| + | |||
| + | <math> F(x) </math> is now in the form of a well known power series. Specifically, the following identity can be used: | ||
| + | <center> <math> \frac{1}{1 - c x} = \Sigma_{n=0}^{\infty}c^n x^n </math> </center> | ||
| + | |||
| + | <math> F(x) </math> can now be rewritten with an explicit formula for the coefficients of the power series: | ||
| + | |||
| + | <center> <math> F(x) = \Sigma_{n=0}^{\infty} F_n x^n = \frac{1}{\sqrt{5}} (\Sigma_{n=0}^{\infty}\phi^n x^n - \Sigma_{n=0}^{\infty}(\frac{1}{\phi})^n x^n) =\Sigma_{n=0}^{\infty} \frac{1}{\sqrt{5}}(\phi^n - (\frac{1}{\phi})^n) x^n</math> </center> | ||
| + | |||
| + | <center> <math> F_n = \frac{1}{\sqrt{5}}(\phi^n - (\frac{1}{\phi})^n) </math> </center> | ||
| + | |||
| + | This method of deriving Binet's formula was largely based off the work of Austin Rochford on the page [https://austinrochford.com/posts/2013-11-01-generating-functions-and-fibonacci-numbers.html "Generating Functions and the Fibonacci Numbers"] <sup>[https://austinrochford.com/posts/2013-11-01-generating-functions-and-fibonacci-numbers.html (13)]</sup>. Although somewhat complicated, this method illuminates exactly how the golden ratio enters into the Fibonacci numbers, and how infinite series can be manipulated to solve various problems. | ||
| + | |||
| + | The following pages explore how these mathematical concepts relate to phyllotaxis, and in what ways the Fibonacci sequence and golden ratio can be found in aspects of plant formation. The Fibonacci numbers appear in nature because their values and their relationship to the golden ratio proves to often be beneficial. | ||
[[Walther MA279 Fall2018 topic1|Back to Home]] | [[Walther MA279 Fall2018 topic1|Back to Home]] | ||
[[Category:MA279Fall2018Walther]] | [[Category:MA279Fall2018Walther]] | ||
Latest revision as of 22:28, 2 December 2018
Introduction
The Fibonacci sequence is one of the more widely known integer sequences used in mathematics. An integer sequence is simply an ordered list of integers (0, ±1, ±2, …). The Fibonacci sequence is typically constructed recursively; the nth term of the sequence can be determined by the previous terms. Beginning with 0 and 1, the Fibonacci sequence is given by:
that is to say that the nth term is the sum of the previous two terms of the sequence (3). The first several Fibonacci numbers are then:
At first glance, the Fibonacci sequence seems relatively benign. However, it is related to many phenomena observed in nature, due to how the sequence can be represented graphically. Consider the rectangle in Figure 1. It has been constructed by combining squares with side lengths equal to the Fibonacci numbers in a cyclical manner. A spiral can be created by drawing a portion of a circle within each square. The result is the Fibonacci spiral, which appears in many plant structures. Specifically, the Fibonacci sequence is prominent in the phyllotaxis, or leaf arrangement, of plants.

The Fibonacci sequence cannot be discussed independently of the golden ratio. The golden ratio, denoted by φ, is equal to:
The value of the golden ratio can be found using a variety of method. For example, consider the golden rectangle seen below.
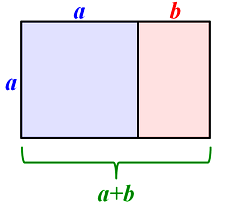
A golden rectangle is constructed by taking a square of side length a, and extending it a length b so that the following is true:
The golden ratio is the value $ \frac{a}{b} $ that solves this equation. If we substitute $ x = \frac{a}{b} $, we can see that only a simple quadratic equation must be solved:
Which has solutions:
The first solution (which is positive) is defined as the golden ratio. The golden ratio is strongly related to the Fibonacci sequence, as the ratio between consecutive terms of the Fibonacci sequence approaches . Consider the ratio between Fn and Fn-1, and between Fn-1 and Fn-2. Since the sequence approaches a fixed ratio, as $ n \rightarrow \infty $, we have:
Using the recursive relationship that defines the Fibonacci series, we can rewrite the above equation as:
Substituting $ x = \frac{F_{n-1}}{F_{n-2}} $, we obtain the same equation as for the golden rectangle:
In fact, the golden ratio can be used to provide an explicit equation for the nth Fibonacci number:
This is known as Binet’s formula (10). The derivation of Binet’s formula involves some clever math involving infinite series. We wish to find a formula $ F(x) $ that yields the $ x^{th} $ Fibonacci number. To begin, we represent $ F(x) $ as a power series with coefficients equal to the $ n^{th} $ Fibonacci number:
Next, we take the recursive relationship that defines the Fibonacci sequence and substitute for $ F_n $:
This expansion makes it clear why the first two terms of the sequence had to be removed from the infinite sum: otherwise $ F_{n-2} $ and $ F_{n-1} $ would not be defined, as $ n $ would be negative. Consider the first sum containing $ F_{n-1} $. It can be rewritten in terms of the original function $ F(x) $ by factoring out x:
For the second sum containing $ F_{n-2} $ we may do the same thing by factoring out $ x^2 $ instead of $ x $:
With some basic algebra, the above expression can be solved for $ F(x) $, yielding:
At this point, it may still seem unclear as to how a formula for the Fibonacci series can be found from the above equation. The goal is to find a formula for the coefficients of the power series used to define $ F(x) $ in terms of $ n $. Since the $ n^{th} $ coefficient of the power series is equal to the $ n^{th} $ Fibonacci number by construction, this will give an explicit formula for the Fibonacci numbers.
The way forward is to somehow express the new equation for $ F(x) $ as a well-known power series. First note that the quadratic polynomial in the denominator of $ F(x) $ is the same as that of the derivation of the golden ratio. $ F(x) $ can then be rewritten as:
The algebra invovled in obtaining the above equation is somewhat complicated, and involves using identies of the golden ratio like $ \phi = \frac{1}{\phi} $ as well as a technique called partial fractions. However, the equivalence of the above expression can be easily verified.
$ F(x) $ is now in the form of a well known power series. Specifically, the following identity can be used:
$ F(x) $ can now be rewritten with an explicit formula for the coefficients of the power series:
This method of deriving Binet's formula was largely based off the work of Austin Rochford on the page "Generating Functions and the Fibonacci Numbers" (13). Although somewhat complicated, this method illuminates exactly how the golden ratio enters into the Fibonacci numbers, and how infinite series can be manipulated to solve various problems.
The following pages explore how these mathematical concepts relate to phyllotaxis, and in what ways the Fibonacci sequence and golden ratio can be found in aspects of plant formation. The Fibonacci numbers appear in nature because their values and their relationship to the golden ratio proves to often be beneficial.

