m |
|||
| (7 intermediate revisions by 2 users not shown) | |||
| Line 3: | Line 3: | ||
=Failure of the models= | =Failure of the models= | ||
''Example of using logistic models to fit U.S. population from 1725 to 1950'' | ''Example of using logistic models to fit U.S. population from 1725 to 1950'' | ||
| + | ---- | ||
We have mentioned the fact that models are not perfectly fitting the population data we have, but by how much and how bad is the projection? In this section, we will be refereeing some real numerical data to support our claims. | We have mentioned the fact that models are not perfectly fitting the population data we have, but by how much and how bad is the projection? In this section, we will be refereeing some real numerical data to support our claims. | ||
| Line 8: | Line 9: | ||
Let’s started with the dataset we will use below, with the initial population in 1700 as 1 million. You can see side by side comparison about how exponential growth model and classic logistic growth model compares with the actual growth number. | Let’s started with the dataset we will use below, with the initial population in 1700 as 1 million. You can see side by side comparison about how exponential growth model and classic logistic growth model compares with the actual growth number. | ||
| − | [[File:Graph_6.1.png|500px]] | + | <center>[[File:Graph_6.1.png|500px]]</center> |
For all the data fitting in this section, we are using David A. Coutts’s article(2011), his sources is Benjamin Franklin's 1751 observation of the population of the USA, How Many People Can The Earth Support by Joel E. Cohen (1995) and "Atlas Of World Population History" by Colin McEvedy and Richard Jones. | For all the data fitting in this section, we are using David A. Coutts’s article(2011), his sources is Benjamin Franklin's 1751 observation of the population of the USA, How Many People Can The Earth Support by Joel E. Cohen (1995) and "Atlas Of World Population History" by Colin McEvedy and Richard Jones. | ||
| Line 18: | Line 19: | ||
The Actual Growth of the population of the USA is based on figures from Colin McEvedy and Richard Jones. | The Actual Growth of the population of the USA is based on figures from Colin McEvedy and Richard Jones. | ||
| − | [[File:Graph_6.2.png|500px]] | + | <center>[[File:Graph_6.2.png|500px]],</center> |
From the graph, we can clearly see that the exponential growth models doesn’t fit the true data. While at the same time, even though it appears to have a closer fit to reality, the logistic model also fails in the prediction. | From the graph, we can clearly see that the exponential growth models doesn’t fit the true data. While at the same time, even though it appears to have a closer fit to reality, the logistic model also fails in the prediction. | ||
| − | Cohen mentions Tuckwell and Koziol’s report (1992, as cited in David, 2011) that promoted the use of the logistic model for population growth predictions around the world. The model was initially successful, but failed following a baby boom post World War II. The report states "...Thus there are apparently logistic-type regimes which persist until some major event occurs." As Cohen (1995, as cited in David, 2011) puts it: | + | Cohen mentions Tuckwell and Koziol’s report (1992, as cited in David, 2011) that promoted the use of the logistic model for population growth predictions around the world. The model was initially successful, but failed following a baby boom post World War II. The report states "...Thus there are apparently logistic-type regimes which persist until some major event occurs." |
| + | |||
| + | As Cohen (1995, as cited in David, 2011) puts it: | ||
"That is, the logistic curve works until it doesn't. The principal assumption of the logistic curve, that the population growth declines in a straight line as the population increases, is flatly contradicted by the increasing population growth rate throughout most of the history of world population up to 1965...." | "That is, the logistic curve works until it doesn't. The principal assumption of the logistic curve, that the population growth declines in a straight line as the population increases, is flatly contradicted by the increasing population growth rate throughout most of the history of world population up to 1965...." | ||
| − | [[ Walther MA279 Fall2018 topic10|Back to Walther MA279 Fall2018 | + | Indeed, predicting the population is very difficult. It’s more than selecting several dots in the data and trying to come up with a fancy model from scratch. It also involves data collecting, analysis and some more advanced math like stochastic process as the real world has so many unexpected things happening that will influence the population size greatly. For curious readers, we have listed some references related to how population projections work in nowadays. |
| + | |||
| + | |||
| + | |||
| + | [[Further_information|Next Section: Further information]] | ||
| + | |||
| + | [[Logistic_Models|Previous Section: Logistic Models]] | ||
| + | |||
| + | [[ Walther MA279 Fall2018 topic10|Back to Walther MA279 Fall2018 Topic10 Home Page]] | ||
Latest revision as of 21:51, 2 December 2018
Failure of the models
Example of using logistic models to fit U.S. population from 1725 to 1950
We have mentioned the fact that models are not perfectly fitting the population data we have, but by how much and how bad is the projection? In this section, we will be refereeing some real numerical data to support our claims.
Let’s started with the dataset we will use below, with the initial population in 1700 as 1 million. You can see side by side comparison about how exponential growth model and classic logistic growth model compares with the actual growth number.
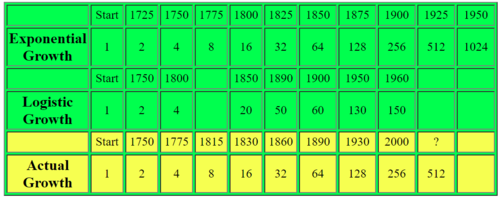
For all the data fitting in this section, we are using David A. Coutts’s article(2011), his sources is Benjamin Franklin's 1751 observation of the population of the USA, How Many People Can The Earth Support by Joel E. Cohen (1995) and "Atlas Of World Population History" by Colin McEvedy and Richard Jones.
For the exponential growth prediction, he assume that double the population needs a period of 25 years, which is equates to an average constant growth rate of 2.8% per annum.
For the Logistic Growth prediction, we assumed an upper asymptote (carrying capacity) of 197.27 million which is set by Pearl and Read (1920)
The Actual Growth of the population of the USA is based on figures from Colin McEvedy and Richard Jones.
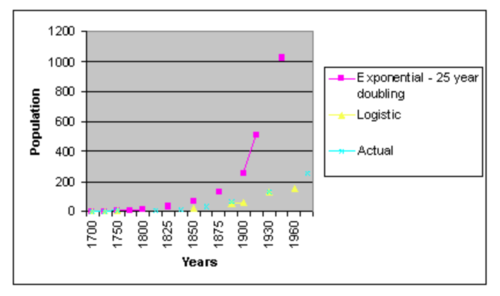 ,
,From the graph, we can clearly see that the exponential growth models doesn’t fit the true data. While at the same time, even though it appears to have a closer fit to reality, the logistic model also fails in the prediction.
Cohen mentions Tuckwell and Koziol’s report (1992, as cited in David, 2011) that promoted the use of the logistic model for population growth predictions around the world. The model was initially successful, but failed following a baby boom post World War II. The report states "...Thus there are apparently logistic-type regimes which persist until some major event occurs."
As Cohen (1995, as cited in David, 2011) puts it: "That is, the logistic curve works until it doesn't. The principal assumption of the logistic curve, that the population growth declines in a straight line as the population increases, is flatly contradicted by the increasing population growth rate throughout most of the history of world population up to 1965...."
Indeed, predicting the population is very difficult. It’s more than selecting several dots in the data and trying to come up with a fancy model from scratch. It also involves data collecting, analysis and some more advanced math like stochastic process as the real world has so many unexpected things happening that will influence the population size greatly. For curious readers, we have listed some references related to how population projections work in nowadays.
Next Section: Further information

