(Created page with "Category:2018 Spring ECE 301 Boutin =Explanation of Sampling Theorem= The sampling theorem: 1. for x(nT) to be equally spaced samples of x(t), while n=0, +1, -1, +2, -...") |
|||
| (5 intermediate revisions by the same user not shown) | |||
| Line 4: | Line 4: | ||
The sampling theorem: | The sampling theorem: | ||
| + | |||
1. for x(nT) to be equally spaced samples of x(t), while n=0, +1, -1, +2, -2, ... | 1. for x(nT) to be equally spaced samples of x(t), while n=0, +1, -1, +2, -2, ... | ||
| + | |||
2. x(t) is band limited. | 2. x(t) is band limited. | ||
| − | X(omega) = 0 for <math>|\omega|>\omega_m | + | X(<math>\omega</math>) = 0 for <math>|\omega|>\omega_m</math> |
| − | + | ||
| + | 3. <math> 2\pi/T = \omega_s > 2\omega_m</math> (Nyquist Condition) | ||
| + | |||
| + | Then x(t) is uniquely recoverable. | ||
| + | |||
| + | Here is a block diagram of sampling and reconstruction using a LPF: | ||
| + | |||
| + | [[File:BlockDSamp.PNG|frameless|left|block diagram of sampling]] | ||
| + | |||
[[ 2018 Spring ECE 301 Boutin|Back to 2018 Spring ECE 301 Boutin]] | [[ 2018 Spring ECE 301 Boutin|Back to 2018 Spring ECE 301 Boutin]] | ||
Latest revision as of 14:13, 30 April 2018
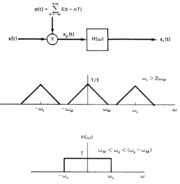
Explanation of Sampling Theorem
The sampling theorem:
1. for x(nT) to be equally spaced samples of x(t), while n=0, +1, -1, +2, -2, ...
2. x(t) is band limited. X($ \omega $) = 0 for $ |\omega|>\omega_m $
3. $ 2\pi/T = \omega_s > 2\omega_m $ (Nyquist Condition)
Then x(t) is uniquely recoverable.
Here is a block diagram of sampling and reconstruction using a LPF: