| (One intermediate revision by the same user not shown) | |||
| Line 79: | Line 79: | ||
\mu_n = \frac{q\tau_n}{m^*}\sim\tau_n | \mu_n = \frac{q\tau_n}{m^*}\sim\tau_n | ||
</math> | </math> | ||
| − | [[Image:MN2_2009_2.png|Alt text| | + | [[Image:MN2_2009_2.png|Alt text|558x336px]] |
------------------------------------------------------------------------------------ | ------------------------------------------------------------------------------------ | ||
4) a) ?? | 4) a) ?? | ||
| − | b) [[Image:MN2_2009_3.png|Alt text| | + | b) [[Image:MN2_2009_3.png|Alt text|678x364px]] |
Depletion mode device is ON without applied <math>V_{GS}</math>. So, <math>V_{GS}</math> is lower for Dep. mode device. Hence low current. | Depletion mode device is ON without applied <math>V_{GS}</math>. So, <math>V_{GS}</math> is lower for Dep. mode device. Hence low current. | ||
Latest revision as of 21:28, 5 August 2017
MICROELECTRONICS and NANOTECHNOLOGY (MN)
Question 2: Junction Devices
August 2009
Questions
All questions are in this link
Solutions of all questions
1) a) Zinc blend crystal. 8 atoms/unit cell. b) $ 1.12 eV $
c) $ \sim10^4 V/cm (??) $
d) Chemistry exam question. (some other language) ??
------------------------------------------------------------------------------------
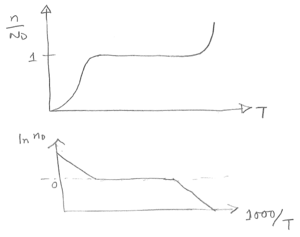
2) a) $ n = N_Ce^{(E_F-E_C)/kT} p = N_Ve^{(E_V-E_F)/kT} $
b) If $ E_F = E_i $ then $ n = n_i, p = n_i $ $ \begin{align*} n_i &= N_Ce^{(E_i-E_C)/kT} =n\\ n_i &= N_Ve^{(E_V-E_i)/kT} =p\\ \therefore n_p&=n_i^2=N_CN_Ve^{-E_g/kT} \end{align*} $
------------------------------------------------------------------------------------
3) a)
$ \begin{align*} p &=\frac{1}{q\mu_nN_D}\\ \implies\mu_n&=\frac{1}{qp\cdot N_D}\sim 1.5\times10^3cm^2/V\cdot s \text{ (chk)} \end{align*} $
b)
$ \mu_p=\frac{1}{qp\cdot N_A}\sim 0.5\times10^3cm^2/V\cdot s \text{ (chk)} $ $ \mu_p<\mu_n $ as $ p_p>p_n $
because $ m_p^*>m_n^* $
c) Ionized impurity
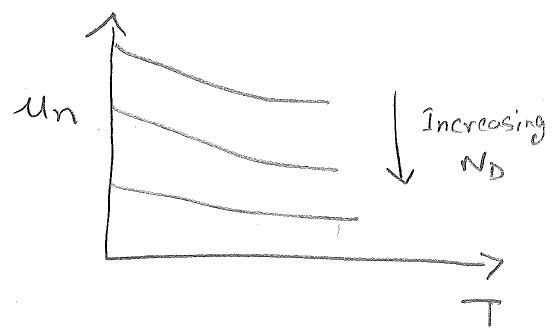
$ \tau_n\sim\frac{T^{3/2}}{N_D} $
Photon scattering
$ \tau_n\sim T^{-3/2} $ $ \mu_n = \frac{q\tau_n}{m^*}\sim\tau_n $
------------------------------------------------------------------------------------ 4) a) ??
b) 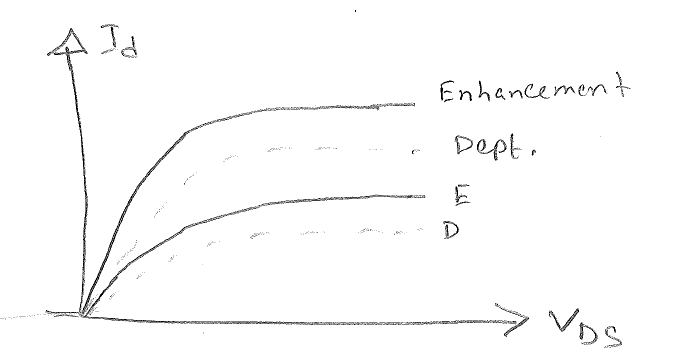 Depletion mode device is ON without applied $ V_{GS} $. So, $ V_{GS} $ is lower for Dep. mode device. Hence low current.
Depletion mode device is ON without applied $ V_{GS} $. So, $ V_{GS} $ is lower for Dep. mode device. Hence low current.
c) $ I_D = \frac{1}{2}\mu_nC_{ox}\frac{W}{L}(V_{GS}-V_{th})^2 $ $ g_m = \frac{\partial I_D}{\partial V_{GS}} = \mu_nC_{ox}\frac{W}{L}(V_{GS}-V_{th}) $ If W=L then; $ \mu_n=\frac{g_m}{C_{ox}(V_{GS}-V_{th})} $
------------------------------------------------------------------------------------